Existential restrictions¶
Prerequesites¶
Qualified existential restrictions¶
Semantics¶
Given
ObjectProperty: r
Class: D
EquivalentTo: r some C
Class: C
the semantics of
r some C is the set of individuals such that for each
individual x there is at least 1 individual y of type C that is linked to
x via the object property r.
Based on this semantics, a possible world adhering to our initial equivalence axiom may be:
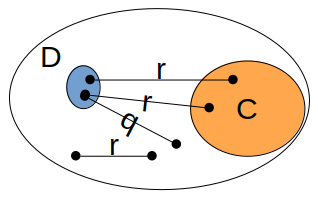
In this Venn diagram we assume individuals are black dots.
Thus, our world consists of 7 individuals,
with only 2 classes, namely C and D, as well 2 object properties, namely r and q.
In this world, D and thus the class r some C, consist of only 2 individuals. D and
r some C consist of only 2 individuals because these are the only individuals linked
via object property r to at least 1 individual respectively in C.
Examples¶
In the following we define a pet owner as someone that owns at least 1 pet.
ObjectProperty: owns
Class: PetOwner
EquivalentTo: owns some Pet
Class: Pet
If we want to introduce the class DogOwner, assuming we can only use the class Pet
and the object property owns (assuming we have not defined PetOwner), we could say
that a dog owner is a subset of pet owners:
ObjectProperty: owns
Class: DogOwner
SubClassOf: owns some Pet
Class: Pet
In this case we use SubClassOf instead of EquivalentTo because not every pet owner
necessarily owns a dog. This is equivalent to stating:
ObjectProperty: owns
Class: PetOwner
EquivalentTo: owns some Pet
Class: Pet
Class: DogOwner
SubClassOf: PetOwner
Variations on existential restrictions¶
Unqualified existential restrictions¶
In the previous section we modeled a PetOwner as owns some Pet. In the expression
owns some Pet Pet is referred to as the filler of owns and more specifically
we say Pet is the owns-filler.
The PetOwner EquivalentTo: owns some Pet state that pet owners are those individuals
that own a pet and ignore all other owns-fillers that are not pets. How can we define
arbitrary ownership?
ObjectProperty: owns
Class: Owner
EquivalentTo: owns some owl:Thing
Value restrictions¶
We can base restrictions on having a relation to a specific named individual, i.e.:
Individual: UK
ObjectProperty: citizenOf
Class: UKCitizen
EquivalentTo: citizenOf hasValue UK
Existential restrictions on data properties¶
This far we have only considered existential restrictions based on object properties, but it is possible to define existential restrictions based on data properties. As an example, we all expect that persons have at least 1 name. This could be expressed as follows:
DataProperty: name
Class: Person
SubClassOf: name some xsd:string
When to use SubClassOf vs EquivalentTo with existential restrictions¶
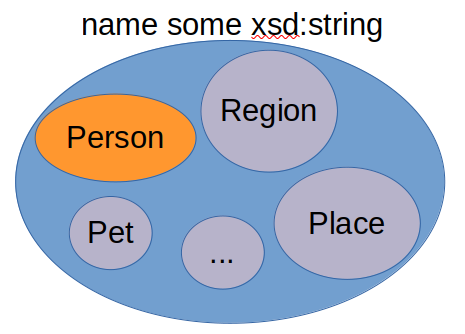
In our example of Person SubClassOf: name some xsd:string, why did we use SubClassOf
rather than EquivalentTo? That is, why did we not use
Person EquivalentTo: name some xsd:string? With using the EquivalentTo axiom, any
individual that has a name, will be inferred to be an instance of Person. However,
there are many things in the world that have names that are not persons. Some examples are pets,
places, regions, etc:
Compare this with, for example, DogOwner:
ObjectProperty: owns
Class: Dog
Class: DogOwner
EquivalentTo: owns some Dog