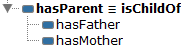Family History Knowledge Base (FHKB) tutorial

Manchester Family History Advanced OWL

This is a fork of the infamous Manchester Family History Advanced OWL Tutorial version 1.1, located at

http://owl.cs.manchester.ac.uk/publications/talks-and-tutorials/fhkbtutorial/

The translation to markdown is not without issue, but we are making a start to making the tutorial a bit more accessible. This reproduction is done with kind permission by Robert Stevens.

Original credits (Version 1.1, see pdf):

Authors:

• Robert Stevens
• Margaret Stevens
• Nicolas Matentzoglu
• Simon Jupp

Bio-Health Informatics Group
School of Computer Science
University of Manchester
Oxford Road
Manchester
United Kingdom
M13 9PL
robert.stevens@manchester.ac.uk

Contributors

• v 1.0 Robert Stevens, Margaret Stevens, Nicolas Matentzoglu and Simon Jupp
• v 1.1 Robert Stevens, Nicolas Matentzoglu
• v 2.0 (Web version) Robert Stevens, Nicolas Matentzoglu, Shawn Tan

The University of Manchester
Copyright© The University of Manchester
November 25, 2015

Acknowledgements

This tutorial was realised as part of the Semantic Web Authoring Tool (SWAT) project (see http://www.swatproject.org), which is supported by the UK Engineering and Physical Sciences Research Council (EPSRC) grant EP/G032459/1, to the University of Manchester, the University of Sussex and the Open University.

Dedication

The Stevens family—all my ancestors were necessary for this to happen. Also, for my Mum who gathered all the information.

Contents

Preamble

• 0.1 Licencing
• 0.2 Reporting Errors
• 0.3 Acknowledgements

1. Introduction

• 1.1 Learning Outcomes
• 1.2 Why Family History?
• 1.3 How to use this Tutorial
• 1.4 FHKB Resources
• 1.5 Conventions used in this Tutorial

2. Adding some Individuals to the FHKB

• 2.1 A World of Objects
• 2.2 Asserting Parentage Facts
• 2.3 Summary

3. Ancestors and Descendants

• 3.1 Ancestors and Descendants
• 3.2 Grandparents and Great Grandparents
• 3.3 Summary

4. Modelling the Person Class

• 4.1 The Class of Person
• 4.2 Describing Sex in the FHKB
• 4.3 Defining Man and Woman
• 4.4 Describing Parentage in the FHKB
• 4.5 Who has a father?
• 4.6 Filling in Domains and Ranges for the FHKB Properties
• 4.7 Inconsistencies
• 4.8 Adding Some Defined Classes for Ancestors and so on
• 4.9 Summary

5. Siblings in the FHKB

• 5.1 Blood relations
• 5.2 Siblings: Option One
• 5.2.1 Brothers and Sisters
• 5.3 Siblings: Option two
• 5.3.1 Which Modelling Option to Choose for Siblings?
• 5.4 Half-Siblings
• 5.5 Aunts and Uncles
• 5.6 Summary

6. Individuals in Class Expressions

• 6.1 Richard and Robert’s Parents and Ancestors
• 6.2 Closing Down What we Know About Parents and Siblings
• 6.3 Summary

7. Data Properties in the FHKB

• 7.1 Adding Some Data Properties for Event Years - 7.1.1 Counting Numbers of Children
• 7.2 The Open World Assumption
• 7.3 Adding Given and Family Names
• 7.4 Summary

8. Cousins in the FHKB

• 8.1 Introducing Cousins
• 8.2 First Cousins
• 8.3 Other Degrees and Removes of Cousin
• 8.4 Doing First Cousins Properly
• 8.5 Summary

9. Marriage in the FHKB

• 9.1 Marriage - 9.1.1 Spouses
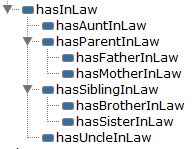
• 9.2 In-Laws
• 9.3 Brothers and Sisters In-Law
• 9.4 Aunts and Uncles in-Law
• 9.5 Summary

10. Extending the TBox

• 10.1 Adding Defined Classes
• 10.2 Summary

11. Final remarks

A FHKB Family Data

All FHKB owl files for download

Preamble

0.1 Licencing

The ‘Manchester Family History Advanced OWL Tutorial’ by Robert Stevens, Margaret Stevens, Nicolas Matentzoglu, Simon Jupp is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

0.2 Reporting Errors

This manual will almost certainly contain errors, defects and infelicities. Do report them to robert.stevens@manchester.ac.uk supplying chapter, section and some actual context in the form of words will help in fixing any of these issues.

0.3 Acknowledgements

As well as the author list, many people have contributed to this work. Any contribution, such as reporting bugs etc., is rewarded by an acknowledgement of contribution (in alphabetical order) when the authors get around to adding them:

• Graham Goff;
• Matthew Horridge;
• Jared Leo;
• Fennie Liang;
• Phil Lord;
• Fiona McNeill;
• Eleni Mikroyannidi;
• George Moulton;
• Bijan Parsia;
• Alan Rector;
• Uli Sattler;
• Dmitry Tsarkov;
• Danielle Welter.

Chapter 1

Introduction

This tutorial introduces the tutee to many of the more advanced features of the Web Ontology Language (OWL). The topic of family history is used to take the tutee through various modelling issues and, in doing so, using many features of OWL 2 to build a Family History Knowledge Base (FHKB). The exercises are designed to maximise inference about family history through the use of an automated reasoner on an OWL knowledge base (KB) containing many members of the Stevens family.

The aim, therefore, is to enable people to learn advanced features of OWL 2 in a setting that involves both classes and individuals, while attempting to maximise the use of inference within the FHKB.

1.1 Learning Outcomes

By doing this tutorial, a tutee should be able to:

1. Know about the separation of entities into TBox and ABox;
2. Use classes and individuals in modelling;
3. Write fancy class expressions;
4. Assert facts about individuals;
5. Use the effects of property hierarchies, property characteristics, domain/range constraints to drive inference;
6. Use constraints and role chains on inferences about individuals;
7. Understand and manage the consequences of the open world assumption in the TBox and ABox;
8. Use nominals in class expressions;
9. Appreciate some limits of OWL 2.

1.2 Why Family History?

Building an FHKB enables us to meet our learning outcomes through a topic that is accessible to virtually everyone. Family history or genealogy is a good topic for a general tutorial on OWL 2 as it enables us to touch many features of the language and, importantly, it is a field that everyone knows. All people have a family and therefore a family history – even if they do not know their particular family history. A small caveat was put on the topic being accessible to everyone as some cultures differ, for instance, in the description of cousins and labels given to different siblings. Nevertheless, family history remains a topic that everyone can talk about.

Family history is a good topic for an OWL ontology as it obviously involves both individuals – the people involved – and classes of individuals – people, men and women, cousins, etc. Also, it is an area rich in inference; from only knowing parentage and sex of an individual, it is possible to work out all family relationships – for example, sharing parents implies a sibling relationship; one’s parent’s brothers are one’s uncles; one’s parent’s parents are one’s grandparents. So, we should be able to construct an ontology that allows us to both express family history, but also to infer family relationships between people from knowing relatively little about them.

As we will learn through the tutorial, OWL 2 cannot actually do all that is needed to create a FHKB. This is unfortunate, but we use it to our advantage to illustrate some of the limitations of OWL 2. We know that rule based systems can do family history with ease, but that is not the point here; we are not advocating OWL DL as an appropriate mechanism for doing family history, but we do use it as a good educational example.

We make the following assumptions about what people know:

• We assume that people know OWL to the level that is known at the end of the Pizza tutorial. Some ground will be covered again, but a lot of basic OWL is assumed.
• We assume people know how to use Protégé or their OWL environment of choice. We do not give ‘click by click’ instructions. At some places, some guidance is given, but this is not to be relied upon as Protégé changes and we will not keep up to date.

We make some simplifying assumptions in this tutorial:

• We take a conventional western view of family history. This appears to have most effects on naming of sibling and cousin relationships.
• We take a straight-forward view on the sex of people; this is explored further in Chapter 4;
• A ‘conventional’ view of marriage is taken; this is explored further in Chapter 9.
• We make no special treatment of time or dates; we are only interested in years and we do not do anything fancy; this is explored more in Chapter 7.
• We assume the ancestors of people go back for ever; obviously this is not true, eventually one would get back to a primordial soup and one’s ancestors are not humans (members of the classPerson), but we don’t bother with such niceties.

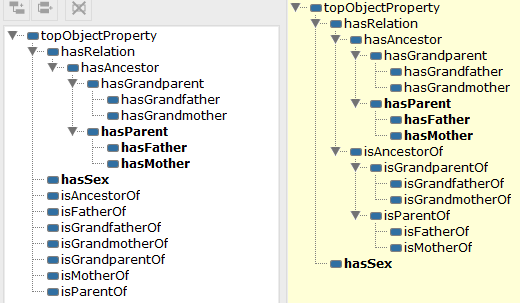
At the end of the tutorial, you should be able to produce a property hierarchy and a TBox or class hierarchy such as shown in Figure 1.1; all supported by use of the automated reasoner and a lot of OWL 2’s features.

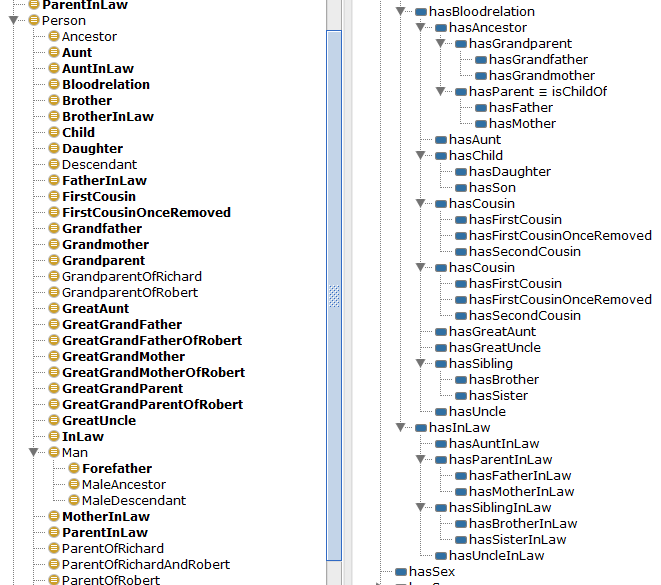
Figure 1.1: A part of the class and property hierarchy of the final FHKB.

1.3 How to use this Tutorial

Here are some tips on using this manual to the best advantage:

• Start at the beginning and work towards the end.
• You can just read the tutorial, but building the FHKB will help you learn much more and much more easily
• Use the reasoner in each task; a lot of the FHKB tutorial is about using the reasoner and not doing so will detract from the learning outcomes.

1.4 FHKB Resources

The following resources are available at http://owl.cs.manchester.ac.uk/tutorials/fhkbtutorial:

• A full version of the Stevens FHKB.
• Some links to papers about the FHKB.
• Some slides about the FHKB tutorial.
• A set of OWL resources for each stage of the FHKB.
• Some blogs about the FHKB are at http://robertdavidstevens.wordpress.com.

1.5 Conventions used in this Tutorial

• All OWL is written in Manchester Syntax.
• When we use FHKB entities within text, we use a sans serif typeface.
• We use CamelCase for classes and property names.
• Class names start with upper case.
• Individual names start with a lower case letter and internal underscores to break words.
• Property names usually start with ‘is’ or ‘has’ and are CamelCase with a lower case initial letter.
• Many classes and individuals in the FHKB have annotation properties, usually human readable labels. They show up in some of the examples in Manchester syntax, but are not made explicit as part of the tasks in this tutorial.
• Every object property is necessarily a sub-property of topObjectProperty. It does not have to be asserted as such. Nevertheless, there might be situations where this relationship is made explicit in this tutorial for illustrative reasons.
• The individuals we are dealing with represent distinct persons. Throughout the tutorial, once the respective axiom is introduced (chapter 7.1.1), the reader should make sure that all his or her individuals are always made distinct, especially when he or she adds a new one.
• At the end of each chapter, we note the Description Logic Language (expressivity) needed to represent the ontology and the reasoning times for a number of state of the art reasoning systems. This should get the reader a sense how difficult the FHKB becomes for reasoners to deal with over time.
• When there is some scary OWL or the reasoner may find the FHKB hard work, you will see a ‘here be dragons’ image.¹

¹ The image comes fromhttp://ancienthomeofdragon.homestead.com/May 2012.

Chapter 2

Adding some Individuals to the FHKB

In this chapter we will start by creating a fresh OWL ontology and adding some individuals that will be surrogates for people in the FHKB. In particular you will:

1. Create a new OWL ontology for the FHKB;
2. Add some individuals that will stand for members of the Stevens family.
3. Describe parentage of people.
4. Add some facts to specific individuals as to their parentage;
5. See the reasoner doing some work.
6. At the moment we will ignore sex; sex will not happen until Chapter 4.

2.1 A World of Objects

The ‘world’² or field of interest we model in an ontology is made up of objects or individuals. Such objects include, but are not limited to:

• People, their pets, the pizzas they eat;
• The processes of cooking pizzas, living, running, jumping, undertaking a journey;
• The spaces within a room, a bowl, an artery;
• The attributes of things such as colour, dimensions, speed, shape of various objects;
• Boundaries, love, ideas, plans, hypotheses.

² we use ‘world’ as a synonym of ‘field of interest’ or ‘domain’. ‘World’ does not restrict us to modelling the physical world outside our consciousness.

We observe these objects, either outside lying around in the world or in our heads. OWL is all about modelling such individuals. Whenever we make a statement in OWL, when we write down an axiom, we are making statements about individuals. When thinking about the axioms in an ontology it is best to think about the individuals involved, even if OWL individuals do not actually appear in the ontology. All through this tutorial we will always be returning to the individuals being described in order to help us understand what we are doing and to help us make decisions about how to do it.

2.2 Asserting Parentage Facts

Biologically, everyone has parents; a mother and a father³. The starting point for family history is parentage; we need to relate the family member objects by object properties. An object property relates two objects, in this case a child object with his or her mother or father object. To do this we need to create three object properties:

Task 1: Creating object properties for parentage
Create a new ontology; Create an object property hasMother; Create a property isMotherOf and give hasMother the InverseOf: isMotherOf; Do the same for the property hasFather; Create a property hasParent; give it the obvious inverse; Make hasMother and hasFather sub-properties of hasParent. Run the reasoner and look at the property hierarchy.

Note how the reasoner has automatically completed the sub-hierarchy for isParentOf: isMotherOf and isFatherOf are inferred to be sub-properties of isParentOf.

The OWL snippet below shows some parentage fact assertions on an individual. Note that rather than being assertions to an anonymous individual via some class, we are giving an assertion to a named individual.

Individual: grant_plinth
Facts: hasFather mr_plinth, hasMother mrs_plinth

³ Don’t quibble; it’s true enough here.

Task 2: Create the ABox

Using the information in Table A.1 (see appendix) about parentage (so the columns about fathers and mothers), enter the fact assertions for the people which appear in rows shaded in grey. We will only use the hasMother and hasFather properties in our fact assertions. You do not need to assert names and birth years yet. This exercise will require you to create an individual for every person we want to talk about, using the Firstname_Secondname_Familyname_Birthyear pattern, as for example in Robert_David_Bright_1965.

While asserting facts about all individuals in the FHKB will be a bit tedious at times, it might be useful to at least do the task for a subset of the family members. For the impatient reader, there is a convenience snapshot of the ontology including the raw individuals available below.

If you are working with Protégé, you may want to look at the Matrix plugin for
Protégé at this point. The plugin allows you to add individuals quickly in the
form of a regular table, and can significantly reduce the effort of adding any type
of entity to the ontology. In order to install the matrix plugin, open Protégé and
go to File » Check for plugins. Select the ‘Matrix Views’ plugin. Click install,
wait until the the installation is confirmed, close and re-open Protégé; go to the
‘Window’ menu item, select ‘Tabs’ and add the ‘Individuals matrix’.

Now do the following:

Task 3: DL queries
Classify the FHKB. Issue the DL query hasFather value David_Bright_1934 and look at the answers (remember to check the respective checkbox in Protégé to include individuals in your query results). Issue the DL query isFatherOf value Robert_David_Bright_1965. Look at the answers. 4. Look at the entailed facts on Robert_David_Bright_1965.

You should find the following:

• David Bright (1934) is the father of Robert David Bright (1965) and Richard John Bright (1962).
• Robert David Bright (1965) has David Bright 1934 as a parent.

Since we have said that isFatherOf has an inverse of hasFather, and we have asserted that Robert_David_Bright_1965 hasFather David_Bright_1934, we have a simple entailment that David_Bright_1934 isFatherOf Robert_David_Bright_1965. So, without asserting the isFatherOf facts, we have been able to ask and get answers for that DL query.

As we asserted that Robert_David_Bright_1965 hasFather David_Bright_1934, we also infer that he hasParent David_Bright_1934; this is because hasParent is the super-property of hasFather and the sub-property implies the super-property. This works all the way up the property tree until topObjectProperty, so all individuals are related by topObjectProperty—this is always true. This implication ‘upwards’ is the way to interpret how the property hierarchies work.

2.3 Summary

We have now covered the basics of dealing with individuals in OWL ontologies. We have set up some properties, but without domains, ranges, appropriate characteristics and then arranged them in a hierarchy. From only a few assertions in our FHKB, we can already infer many facts about an individual: Simple exploitation of inverses of properties and super-properties of the asserted properties.

We have also encountered some important principles:

• We get inverses for free.
• The sub-property implies the super-property. So, hasFather implies the hasParent fact between individuals. This entailment of the super-property is very important and will drive much of the inference we do with the FHKB.
• Upon reasoning we get the inverses of properties between named individuals for free.
• Lots is still open. For example, we do not know the sex of individuals and what other children, other than those described, people in the FHKB may have.

The FHKB ontology at this stage of the tutorial has an expressivity of ALHI.

The time to reason with the FHKB at this point (in Protégé) on a typical desktop
machine by HermiT 1.3.8 is approximately 0.026 sec (0.00001 % of final), by Pellet
2.2.0 0.144 sec (0.00116 % of final) and by FaCT++ 1.6.4 is approximately 0.
sec (0.000 % of final). 0 sec indicates failure or timeout.

Chapter 3

Ancestors and Descendants

In this Chapter you will:

1. Use sub-properties and the transitive property characteristic to infer ancestors of people;
2. Add properties to the FHKB property hierarchy that will infer ancestors and descendants of a person without adding any more facts to the FHKB;
3. Explore the use of sub-property chains for grandparents, great grandparents and so on;
4. Place all of these new object properties in the property hierarchy and in that way learn more about the implications of the property hierarchy.

Find a snapshot of the ontology at this stage below.

3.1 Ancestors and Descendants

The FHKB has parents established between individuals and we know that all people have two parents. A parent is an ancestor of its children; a person’s parent’s parents are its ancestors; and so on. So, in our FHKB, Robert’s ancestors are David, Margaret, William, Iris, Charles, Violet, James, another Violet, another William, Sarah and so on. If my parent’s parents are my ancestors, then what we need is a transitive version of the hasParent property. Obviously we do not want hasParent to be transitive, as Robert’s grandparents (and so on) would become his parents (and that would be wrong).

We can easily achieve what is necessary. We need a hasAncestor property that has a transitive characteristic. The trick is to make this a super-property of the hasParent property. As explained before, a sub-property implies its super-property. So, if individual x holds a hasParent property with an individual y , then it also holds an instance of its super-property hasAncestor with the individual y. If individual y then holds a hasParent property with another individual z , then there is also, by implication, a hasAncestor property between y and z. As hasAncestor is transitive, x and z also hold a hasAncestor relationship between them.

The inverse of hasAncestor can either be isAncestorOf or hasDescendant. We choose the isAncestorOf option.

Task 4: Object properties: exploiting the semantics

Make a new object property hasRelation, make it symmetric. Make a new object property hasAncestor. Make it a sub-property of hasRelation and a super-property of hasParent. Make hasAncestor transitive. Create the inverse isAncestorOf. Do not ‘stitch’ it into the property hierarchy; the reasoner will sort it all out for you. Run the reasoner and issue the DL query hasAncestor value William_George_Bright_1901. Issue the query isAncestorOf value Robert_David_Bright_1965.

The hasAncestor object property will look like this:

ObjectProperty: hasAncestor
SubPropertyOf: hasRelation
SuperPropertyOf: hasParent,
Characteristics: Transitive
InverseOf: isAncestorOf

As usual, it is best to think of the objects or individuals involved in the relationships. Consider the three individuals – Robert, David and William. Each has a hasFather property, linking Robert to David and then David to William. As hasFather implies its super-property hasParent, Robert also has a hasParent property with David, and David has a hasParent relation to William. Similarly, as hasParent implies hasAncestor, the Robert object has a hasAncestor relation to the David object and the David object has one to the William object. As hasAncestor is transitive, Robert not only holds this property to the David object, but also to the William object (and so on back through Robert’s ancestors).

3.2 Grandparents and Great Grandparents

We also want to use a sort of restricted transitivity in order to infer grandparents, great grandparents and so on. My grandparents are my parent’s parents; my grandfathers are my parent’s fathers. My great grandparents are my parent’s parent’s parents. My great grandmothers are my parent’s parent’s mothers. This is sort of like transitivity, but we want to make the paths only a certain length and, in the case of grandfathers, we want to move along two relationships – hasParent and then hasFather.

We can do this with OWL 2’s sub-property chains. The way to think about sub-property chains is: If we see property x followed by property y linking three objects, then it implies that property z is held between

Figure 3.1: Three blobs representing objects of the classPerson. The three objects are linked by a hasParent property and this implies a hasGrandparent property.

the first and third objects. Figure 3.1 shows this diagrammatically for the hasGrandfather property.

For various grandparent object properties we need the following sets of implications:

• My parent’s parents are my grandparents;
• My parent’s fathers are my grandfathers;
• My parent’s mothers are my grandmothers;
• My parent’s parent’s parents are my great grandparents or my grandparent’s parents are my great grandparents.
• My parent’s parent’s fathers are my great grandfathers or my parent’s grandfathers are my great grandfathers;
• My parent’s parent’s mothers are my great grandmothers (and so on).

Notice that we can trace the paths in several ways, some have more steps than others, though the shorter paths themselves employ paths. Tracing these paths is what OWL 2’s sub-property chains achieve. For the new object property hasGrandparent we write:

ObjectProperty: hasGrandparent SubPropertyChain: hasParent o hasParent

We read this as ‘hasParent followed by hasParent implies hasGrandparent’. We also need to think where the hasGrandparent property fits in our growing hierarchy of object properties. Think about the implications: Does holding a hasParent property between two objects imply that they also hold a hasGrandparent property? Of course the answer is ‘no’. So, this new property is not a super-property of hasParent. Does the holding of a hasGrandparent property between two objects imply that they also hold an hasAncestor property? The answer is ‘yes’; so that should be a super-property of hasGrandparent. We need to ask such questions of our existing properties to work out where we put it in the object property hierarchy. At the moment, our hasGrandparent property will look like this:

ObjectProperty: hasGrandParent
SubPropertyOf: hasAncestor
SubPropertyChain: hasParent o hasParent
SuperPropertyOf: hasGrandmother, hasGrandfather
InverseOf: isGrandParentOf

Do the following task:

Task 5: Grandparents object properties
Make the hasGrandparent, hasGrandmother and hasGrandfather object properties and the obvious inverses (see OWL code above); Go to the individuals tabs and inspects the inferred object property assertions for Robert_David_Bright_1965 and his parents.

Again, think of the objects involved. We can take the same three objects as before: Robert, David and William. Think about the properties that exist, both by assertion and implication, between these objects. We have asserted only hasFather between these objects. The inverse can be inferred between the actual individuals (remember that this is not the case for class level restrictions – that all instances of a class hold a property does not mean that the filler objects at the other end hold the inverse; the quantification on the restriction tells us this). Remember that:

1. Robert holds a hasFather property with David;
2. David holds a hasFather property with William;
3. By implication through the hasParent super-property of hasFather, Robert holds a hasParent property with David, and the latter holds one with William;
4. The sub-property chain on hasGrandfather then implies that Robert holds a hasGrandfather property to William. Use the diagram in figure 3.1 to trace the path; there is a hasParent path from Robert to William via David and this implies the hasGrandfather property between Robert and William.

It is also useful to point out that the inverse of hasGrandfather also has the implication of the sub-property chain of the inverses of hasParent. That is, three objects linked by a path of two isParentOf properties implies that an isGrandfatherOf property is established between the first and third object, in this case William and Robert. As the inverses of hasFather are established by the reasoner, all the inverse implications also hold.

3.3 Summary

It is important when dealing with property hierarchies to think in terms of properties between objects and of the implications ‘up the hierarchy’. A sub-property implies its super-property. So, in our FHKB, two person objects holding a hasParent property between them, by implication also hold an hasAncestor property between them. In turn, hasAncestor has a super-property hasRelation and the two objects in question also hold, by implication, this property between them as well.

We made hasAncestor transitive. This means that my ancestor’s ancestors are also my ancestors. That a sub-property is transitive does not imply that its super-property is transitive. We have seen that by manipulating the property hierarchy we can generate a lot of inferences without adding any more facts to the individuals in the FHKB. This will be a feature of the whole process – keep the work to the minimum (well, almost).

In OWL 2, we can also trace ‘paths’ around objects. Again, think of the objects involved in the path of properties that link objects together. We have done simple paths so far – Robert linked to David via hasParent and David linked to William via hasFather implies the link between Robert and William of hasGrandfather. If this is true for all cases (for which you have to use your domain knowledge), one can capture this implication in the property hierarchy. Again, we are making our work easier by adding no new explicit facts, but making use of the implication that the reasoner works out for us.

The FHKB ontology at this stage of the tutorial has an expressivity ofALRI+.

The time to reason with the FHKB at this point (in Protégé) on a typical desktop
machine by HermiT 1.3.8 is approximately 0.262 sec (0.00014 % of final), by Pellet
2.2.0 0.030 sec (0.00024 % of final) and by FaCT++ 1.6.4 is approximately 0.004
sec (0.000 % of final). 0 sec indicates failure or timeout.

Chapter 4

Modelling the Person Class

In this Chapter you will:

1. Create a Person class;
2. Describe Sex classes;
3. Define Man and Woman;
4. Ask which of the people in the FHKB has a father.
5. Add domains and ranges to the properties in the FHKB.
6. Make the FHKB inconsistent.
7. Add some more defined classes about people and see some equivalence inferred between classes.

These simple classes will form the structure for the whole FHKB.

4.1 The Class of Person

For the FHKB, we start by thinking about the objects involved

1. The people in a family – Robert, Richard, David, Margaret, William, Iris, Charles, Violet, Eileen, John and Peter;
2. The sex of each of those people;
3. The marriages in which they participated;
4. The locations of their births;
5. And many more...

There is a class of Person that we will use to represent all these people objects.

Task 6: Create the Person class
Create a class called DomainEntity; Create a subclass of DomainEntity called Person.

We use DomainEntity as a house-keeping measure. All of our ontology goes underneath this class. We can put other classes ‘outside’ the ontology, as siblings of DomainEntity, such as ‘probe’ classes we wish to use to test our ontology.

The main thing to remember about the Person class is that we are using it to represent all ‘people’ individuals. When we make statements about the Person class, we are making statements about all ‘people’ individuals.

What do we know about people? All members of the Person class have:

• Sex – they are either male or female;
• Everyone has a birth year;
• Everyone has a mother and a father.

There’s a lot more we know about people, but we will not mention it here.

4.2 Describing Sex in the FHKB

Each and every person object has a sex. In the FHKB we will take a simple view on sex – a person is either male or female, with no intersex or administrative sex and so on. Each person only has one sex.

We have two straight-forward options for modelling sex:

1. Each person object has their own sex object, which is either male or female. Thus Robert’s maleness is different from David’s maleness.
2. There is only one Maleness object and one Femaleness object and each person object has a relationship to either one of these sex objects, but not both.

We will take the approach of having a class of Maleness objects and a class of Femaleness objects. These are qualities or attributes of self-standing objects such as a person. These two classes are disjoint, and each is a subclass of a class called Sex. The disjointness means that any one instance of Sex cannot be both an instance of Maleness and an instance of Femaleness at once. We also want to put in a covering axiom on the class Sex, which means that any instance of Sex must be either Maleness or Femaleness; there is no other kind of Sex.

Again, notice that we have been thinking at the level of objects. We do the same when thinking about Person and their Sex. Each and every person is related to an instance of Sex. Each Person holds one relationship to a Sex object. To do this we create an object property called hasSex. We make this property functional, which means that any object can hold that property to only one distinct filler object.

We make the domain of hasSex to be Person and the range to be Sex. The domain of Person means that any object holding that property will be inferred to be a member of the class Person. Putting the range of Sex on the hasSex property means that any object at the right-hand end of the hasSex property will be inferred to be of the class Sex. Again, think at the level of individuals or objects.

We now put a restriction on the Person class to state that each and every instance of the class Person holds a hasSex property with an instance of the Sex class. It has an existential operator ‘some’ in the axiom, but the functional characteristic means that each Person object will hold only one hasSex property to a distinct instance of a Sex object⁴.

⁴ An individual could hold two hasSex properties, as long as the sex objects at the right-hand end of the property are not different.

Task 7: Modelling sex

Create a class called Sex; Make it a subclass of DomainEntity; Make Person and Sex disjoint; Create two subclasses of Sex, Maleness and Femaleness; Make Maleness and Femaleness disjoint; Put a covering axiom on Sex such that it is equivalent to Maleness or Femaleness. Create an object property, hasSex , with the domain Person, the range Sex and give it the characteristic of ‘Functional’; Add a restriction hasSex some Sex to the class Person.

The hasSex property looks like:

ObjectProperty: hasSex
Characteristics: Functional
Domain: Person
Range: Sex

The Person class looks like:

Class: Person
SubClassOf: DomainEntity,(hasSex some Sex)
DisjointWith: Sex

4.3 Defining Man and Woman

We now have some of the foundations for the FHKB. We have the concept of Person, but we also need to have the concepts of Man and Woman. Now we have Person, together with Maleness and Femaleness, we have the necessary components to define Man and Woman. These two classes can be defined as: Any Person object that has a male sex can be recognised to be a man; any Person object that has a female sex can be recognised as a member of the class woman. Again, think about what conditions are sufficient for an object to be recognised to be a member of a class; this is how we create defined classes through the use of OWL equivalence axioms.

To make the Man and Woman classes do the following:

Task 8: Describe men and women
Create a class Man; Make it equivalent to a Person that hasSex some Maleness; Do the same, but with Femaleness, to create the Woman class; A covering axiom can be put on the Person class to indicate that man and woman are the only kinds of person that can exist. (This is not strictly true due to the way Sex has been described.) Run the reasoner and take a look.

Having run the reasoner, the Man and Woman classes should appear underneath Person⁵.

⁵Actually in Protégé, this might happen without the need to run the reasoner.

The Man and Woman classes will be important for use as domain and range constraints on many of the properties used in the FHKB. To achieve our aim of maximising inference, we should be able to infer that individuals are members of Man, Woman or Person by the properties held by an object. We should not have to state the type of an individual in the FHKB.

The classes for Man and Woman should look like:

Class: Man
EquivalentTo: Person and (hasSex some Maleness)

Class: Woman
EquivalentTo: Person and (hasSex some Femaleness)

4.4 Describing Parentage in the FHKB

To finish off the foundations of the FHKB we need to describe a person object’s parentage. We know that each and every person has one mother and each and every person has one father. Here we are talking about biological mothers and fathers. The complexities of adoption and step parents are outside the scope of this FHKB tutorial.

Task 9: Describing Parentage
Add the domain Person and the range Woman to the property hasMother. Do the same for the property hasFather, but give it the range Man; Give the property hasParent domain and range of Person; Run the reasoner.

The (inferred) property hierarchy in the FHKB should look like that shown in Figure 4.1. Notice that we have asserted the sub-property axioms on one side of the property hierarchy. Having done so, the reasoner uses those axioms, together with the inverses, to work out the property hierarchy for the ‘other side’.

We make hasMother functional, as any one person object can hold only one hasMother property to a distinct Woman object. The range of hasMother is Woman, as a mother has to be a woman. The Person object holding the hasMother property can be either a man or a woman, so we have the domain constraint as Person; this means any object holding a hasMother property will be inferred to be a Person. Similarly, any object at the right-hand end of a hasMother property will be inferred to be a Woman, which is the result we need. The same reasoning goes for hasFather and hasParent, with the sex constraints on the latter being only Person. The inverses of the two functional sub-properties of hasParent are not themselves functional. After all, a Woman can be the mother of many Person objects, but each Person object can have only one mother.

Figure 4.1: The property hierarchy with the hasSex and the parentage properties

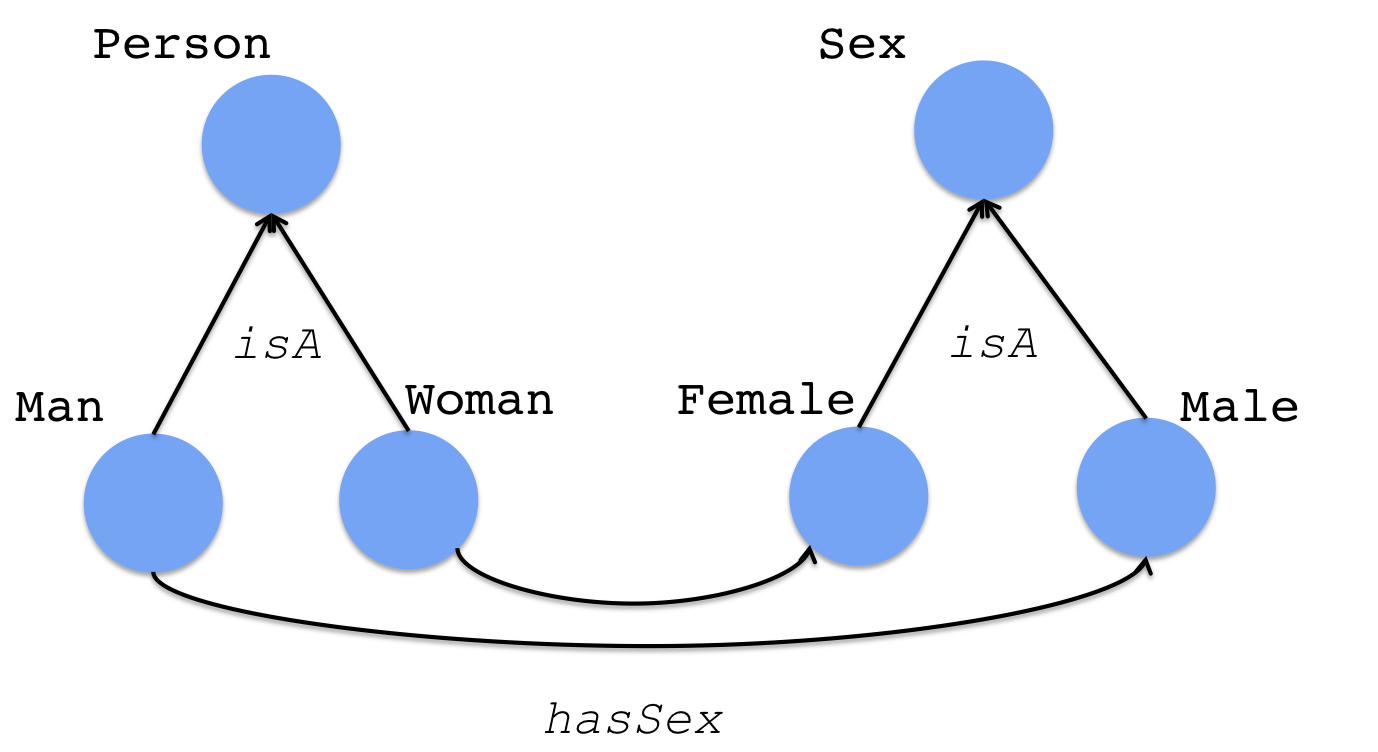
Figure 4.2: the core TBox for the FHKB with the Person and Sex classes.

Task 10: Restrict Person class
As each and every person has a mother and each and every person has a father, place restrictions on the Person class as shown below.

Class: Person
SubClassOf: DomainEntity, (hasFather some Man), (hasMother some Woman),
(hasSex some Sex)
DisjointWith: Sex

Task 11: DL queries for people and sex
Issue the DL queries for Person, Man and Woman; look at the answers and count the numbers in each class; which individuals have no sex and why? You should find that many people have been inferred to be either Man or Woman, but some are, as we will see below, only inferred to be Person.

The domain and range constraints on our properties have also driven some entailments. We have not asserted that David_Bright_1934 is a member of Man, but the range constraint on hasFather (or the inferred domain constraint on the isFatherOf relation) has enabled this inference to be made. This goes for any individual that is the right-hand-side (either inferred or asserted) of either hasFather or hasMother (where the range is that of Woman). For Robert David Bright, however, he is only the left-hand-side of an hasFather or an hasMother property, so we’ve only entailed that this individual is a member of Person.

4.5 Who has a father?

In our description of the Person class we have said that each and every instance of the class Person has a father (the same goes for mothers). So, when we ask the query ‘which individuals have a father’, we get all the instances of Person back, even though we have said nothing about the specific parentage of each Person. We do not know who their mothers and fathers are, but we know that they have one of each. We know all the individuals so far entered are members of the Person class; when asserting the type to be either Man or Woman (each of which is a subclass of Person), we infer that each is a person. When asserting the type of each individual via the hasSex property, we know each is a Person, as the domain of hasSex is the Person class. As we have also given the right-hand side of hasSex as either Maleness or Femaleness, we have given sufficient information to recognise each of these Person instances to be members of either Man or Woman.

4.6 Filling in Domains and Ranges for the FHKB Properties

So far we have not systematically added domains and ranges to the properties in the FHKB. As a reminder, when a property has a domain of X any object holding that property will be inferred to be a member of class X. A domain doesn’t add a constraint that only members of class X hold that property; it is a strong implication of class membership. Similarly, a property holding a range implies that an object acting as right-hand-side to a property will be inferred to be of that class. We have already seen above that we can use domains and ranges to imply the sex of people within the FHKB.

Do the following:

Task 12: Domains and Ranges
Make sure the appropriate Person, Man and Woman are domains and ranges for hasFather, hasMother and hasParent. Run the reasoner and look at the property hierarchy. Also look at the properties hasAncestor, hasGrandparent, hasUncle and so on; look to see what domains and ranges are found. Add any domains and ranges explicitly as necessary.

Protégé for example in its current version (November 2015) does not visualise
inherited domains and ranges in the same way as it shows inferred inverse relations.

We typically assert more domains and ranges than strictly necessary. For example, if we say that hasParent has the domain Person, this means that every object x that is connected to another object y via the hasParent relation must be a Person. Let us assume the only thing we said about x and y is that they are connected by a hasMother relation. Since this implies that x and y are also connected by a hasParent relation (hasMother is a sub-property of hasParent) we do not have to assert that hasFather has the domain of Person; it is implied by what we know about the domain and range of hasParent.

In order to remove as many assertions as possible, we may therefore choose to assert as much as we know starting from the top of the hierarchy, and only ever adding a domain if we want to constrain the already inferred domain even further (or range respectively). For example, in our case, we could have chosen to assert Person to be the domain of hasRelation. Since hasRelation is symmetric, it will also infer Person to be the range. We do not need to say anything for hasAncestor or hasParent, and only if we want to constrain the domain or range further (like in the case of hasFather by making the range Man) do we need to actually assert something. It is worth noting that because we have built the object property hierarchy from the bottom (hasMother etc.) we have ended up asserting more than necessary.

4.7 Inconsistencies

From the Pizza Tutorial and other work with OWL you should have seen some unsatisfiabilities. In Protégé this is highlighted by classes going ‘red’ and being subclasses ofNothing; that is, they can have no instances in that model.

Task 13: Inconsistencies
Add the fact Robert_David_Bright_1965 hasMother David_Bright_1934. Run the classifier and see what happens. Remove that fact and run the classifier again. Now add the fact that Robert_David_Bright_1965 hasMother Iris_Ellen_Archer_1907 Run the classifier and see what happens. Add and remove the functional characteristic to these properties and see what happens.

After asserting the first fact it should be reported by the reasoner that the ontology is inconsistent. This means, in lay terms, that the model you’ve provided in the ontology cannot accommodate the facts you’ve provided in the fact assertions in your ABox—that is, there is an inconsistency between the facts and the ontology... The ontology is inconsistent because David_Bright_1934 is being inferred to be a Man and a Woman at the same time which is inconsistent with what we have said in the FHKB.

When we, however, say that Robert David Bright has two different mothers, nothing bad happens! Our domain knowledge says that the two women are different, but the reasoner does not know this as yet... ; Iris Ellen Archer and Margaret Grace Rever may be the same person; we have to tell the reasoner that they are different. For the same reason the functional characteristic also has no effect until the reasoner ‘knows’ that the individuals are different. We will do this in Section 7.1.1 and live with this ‘fault’ for the moment.

4.8 Adding Some Defined Classes for Ancestors and so on

Task 14: Adding defined classes
Add a defined class for Ancestor, MaleAncestor, FemaleAncestor; Add a defined class for Descendant, MaleDescendant and FemaleDescendant; Run the reasoner and view the resulting hierarchy.

The code for the classes looks like:

Class: Ancestor EquivalentTo: Person and isAncestorOf some Person
Class: FemaleAncestor EquivalentTo: Woman and isAncestorOf some Person
Class: Descendant EquivalentTo: Person and hasAncestor some Person
Class: MaleDescendant EquivalentTo: Man and hasAncestor some Person

The TBox after reasoning can be seen in Figure 4.3. Notice that the reasoner has inferred that several of the classes are equivalent or ‘the same’. These are: Descendant and Person; MaleDescendant and Man, FemaleDescendant and Woman.

The reasoner has used the axioms within the ontology to infer that all the instances of Person are also instances of the class Descendant and that all the instances of Woman are also the same instances as the class Female Descendant. This is intuitively true; all people are descendants – they all have parents that have parents etc. and thus everyone is a descendant. All women are female people that have parents etc. As usual we should think about the objects within the classes and what we know about them. This time it is useful to think about the statements we have made about Person in this Chapter – that all instances of Person have a father and a mother; add to this the information from the property hierarchy and we know that all instances of Person have parents and ancestors. We have repeated all of this in our new defined classes for Ancestor and Descendant and the reasoner has highlighted this information.

Figure 4.3: The defined classes from Section 4.8 in the FHKB’s growing class hierarchy

Task 15: More Ancestors

Query for MaleDescendant. You should get Man back - they are equivalent (and this makes sense). As an additional exercise, also add in properties for forefathers and foremothers. You will follow the same pattern as for hasAncestor, but adding in, for instance, hasFather as the sub-property of the transitive super-property of hasForefather and setting the domains and ranges appropriately (or working out if they’ll be inferred appropriately). Here we interpret a forefather as one’s father’s father etc. This isn’t quite right, as a forefather is any male ancestor, but we’ll do it that way anyway. You might want to play around with DL queries. Because of the blowup in inferred relationships, we decided to not include this pattern in the tutorial version of the FHKB.

4.9 Summary

Most of what we have done in this chapter is straight-forward OWL, all of which would have been met in the pizza tutorial. It is, however, a useful revision and it sets the stage for refining the FHKB. Figure 4.2 shows the basic set-up we have in the FHKB in terms of classes; we have a class to represent person, man and woman, all set-up with a description of sex, maleness and femaleness. It is important to note, however, the approach we have taken: We have always thought in terms of the objects we are modelling.

Here are some things that should now be understood upon completing this chapter:

1. Restrictions on a class in our TBox mean we know stuff about individuals that are members of that class, even though we have asserted no facts on those individuals. We have said, for instance, that all members of the class Person have a mother, so any individual asserted to be a Person must have a mother. We do not necessarily know who they are, but we know they have one.
2. Some precision is missing – we only know Robert David Bright is a Person, not that he is a Man. This is because, so far, he only has the domain constraint of hasMother and hasFather to help out.
3. We can cause the ontology to be inconsistent, for example by providing facts that cannot be accommodated by the model of our ontology. In the example, David Bright was inferred to be a member of two disjoint classes.

Finally, we looked at some defined classes. We inferred equivalence between some classes where the extents of the classes were inferred to be the same – in this case the extents of Person and Descendant are the same. That is, all the objects that can appear in Person will also be members of Descendant. We can check this implication intuitively – all people are descendants of someone. Perhaps not the most profound inference of all time, but we did no real work to place this observation in the FHKB.

This last point is a good general observation. We can make the reasoner do work
for us. The less maintenance we have to do in the FHKB the better. This will be
a principle that works throughout the tutorial.

The FHKB ontology at this stage of the tutorial has an expressivity of SRIF.

The time to reason with the FHKB at this point (in Protégé) on a typical desktop
machine by HermiT 1.3.8 is approximately 0.884 sec (0.00047 % of final), by Pellet
2.2.0 0.256 sec (0.00207 % of final) and by FaCT++ 1.6.4 is approximately 0.013
sec (0.000 % of final). 0 sec indicates failure or timeout.

Chapter 5

Siblings in the FHKB

In this chapter you will:

1. Explore options for determining finding siblings;
2. Meet some of the limitations in OWL;
3. Choose one of the options explored;
4. Add facts for siblings;
5. Use sub-property chains to find aunts and uncles;

Find a snapshot of the ontology at this stage below.

5.1 Blood relations

Do the following first:

Task 16: The bloodrelation object property
Create an hasBloodrelation object property, making it a sub-property of hasRelation. Add appropriate property characteristics. Make the already existing hasAncestor property a sub-property of hasBloodrelation.

Does a blood relation of Robert have the same relationship to Robert (symmetry)? Is a blood relation of Robert’s blood relation a blood relation of Robert (transitivity)? Think of an aunt by marriage; her children are my cousins and blood relations via my uncle, but my aunt is not my blood relation. My siblings share parents; male siblings are brothers and female siblings are sisters. So far we have asserted parentage facts for the Person in our ABox. Remember that our parentage properties have inverses, so if we have added an hasFather property between a Person and a Man, we infer the isFatherOf property between that Man and that Person.

5.2 Siblings: Option One

We should have enough information within the FHKB to infer siblings. We could use a sub-property chain such as:

ObjectProperty: hasSibling
SubPropertyOf: hasBloodrelation
Characteristics: Symmetric, transitive
SubPropertyChain: hasParent o isParentOf

We make a property of hasSibling and make it a sub-property of hasBloodrelation. Remember, think of the objects involved and the implications we want to follow; being a sibling implies being a blood relation, it does not imply any of the other relationships we have in the FHKB.

Note that we have made hasSibling symmetric; if Robert is sibling of Richard, then Richard is sibling of Robert. We should also think about transitivity; if David is sibling of Peter and Peter is sibling of John, then David is sibling of John. So, we make hasSibling symmetric and transitive (see Figure 5.1). However, we must take care of half-siblings: child 1 and child 2 share a mother, but not a father; child 2 and child 3 share the father, but not the mother – child 1 and child 3 are not even half-siblings. However, at least for the moment, we will simply ignore this inconvenience, largely so that we can explore what happens with different modelling options.

Figure 5.1: Showing the symmetry and transitivity of the hasSibling (siblingof) property by looking at the brothers David, John and Peter

We also have the implication using three objects (see Figure 5.2):

1. Robert holds a hasParent property with David;
2. David holds an isFatherOf property with Richard;
3. This implies that Robert holds a hasSibling property with Richard;
4. As hasSibling is symmetric, Richard holds an hasSibling property with Robert.

Figure 5.2: Tracing out the sub-property chain for hasSibling; note that Robert is a sibling of himself by this path

Do the following tasks:

Task 17: Siblings
Add the hasSibling property as above; Run the reasoner; Ask the DL query hasSibling value Robert_David_Bright_1965.

From this last DL query you should get the answer that both Robert and Richard are siblings of Robert. Think about the objects involved in the sub-property chain: we go from Robert to David via the hasParent and from David to Richard via the isParentOf property; so this is OK. However, we also go from Robert to David and then we can go from David back to Robert again – so Robert is a sibling of Robert. We do not want this to be true.

We can add another characteristic to the hasSibling property, the one of being irreflexive. This means that an object cannot hold the property with itself.

Task 18: More siblings
Add the irreflexive characteristic to the hasSibling property; Run the reasoner;

Note that the reasoner claims you have an inconsistent ontology (or in some cases, you might get a message box saying "Reasoner died"). Looking at the hasSibling property again, the reason might not be immediately obvious. The reason for the inconsistency lies in the fact that we create a logical contradiction: through the property chain, we say that every Person is a sibling of him or herself, and again disallowing just that by adding the irreflexive characteristic. A different explanation lies within the OWL specification itself: In order to maintain decidability irreflexive properties must be simple - for example, they may not be property chains⁶.

⁶ http://www.w3.org/TR/owl2-syntax/#The_Restrictions_on_the_Axiom_Closure

5.2.1 Brothers and Sisters

We have only done siblings, but we obviously need to account for brothers and sisters. In an analogous way to motherhood, fatherhood and parenthood, we can talk about sex specific sibling relationships implying the sex neutral hasSibling; holding either a hasBrother or an isSisterOf between two objects would imply that a hasSibling property is also held between those two objects. This means that we can place these two sex specific sibling properties below hasSibling with ease. Note, however, that unlike the hasSibling property, the brother and sister properties are not symmetric. Robert hasBrother Richard and vice versa , but if Daisy hasBrother William, we do not want William to hold an hasBrother property with Daisy. Instead, we create an inverse of hasBrother, isBrotherOf, and the do the same for isSisterOf.

We use similar, object based, thought processes to choose whether to have transitivity as a characteristic of hasBrother. Think of some sibling objects or individuals and place hasBrother properties between them. Make it transitive and see if you get the right answers. Put in a sister to and see if it stil works. If David hasBrother Peter and Peter hasBrother John, then David hasBrother John; so, transitivity works in this case. Think of another example. Daisy hasBrother Frederick, and Frederick hasBrother William, thus Daisy hasBrother William. The inverses work in the same way; William isBrotherOf Frederick and Frederick isBrotherOf Daisy; thus William isBrotherOf Daisy. All this seems reasonable.

Task 19: Brothers and sisters
Create the hasBrother object property as shown below; Add hasSister in a similar manner; 3. Add appropriate inverses, domains and ranges.

ObjectProperty: hasBrother
SubPropertyOf: hasSibling
Characteristics: Transitive
InverseOf: isBrotherOf
Range: Man

We have some hasSibling properties (even if they are wrong). We also know the sex of many of the people in the FHKB through the domains and ranges of properties such as hasFather, hasMother and their inverses..

Can we use sub-property chains in the same way as we have used them in the hasSibling property? The issue is that of sex; the property isFatherOf is sex neutral at the child end, as is the inverse hasFather (the same obviously goes for the mother properties). We could use a sub-property chain of the form:

ObjectProperty: hasBrother
SubPropertyChain: hasParent o hasSon

A son is a male child and thus that object is a brother of his siblings. At the moment we do not have son or daughter properties. We can construct a property hierarchy as shown in Figure 5.3. This is made up from the following properties:

• hasChild and isChildOf
• hasSon(range Man and domain Person) and isSonOf;
• hasDaughter(range Woman domain Person) and isDaughterOf

Note that hasChild is the equivalent of the existing property isParentOf; if I have a child, then I am its parent. OWL 2 can accommodate this fact. We can add an equivalent property axiom in the following way:

ObjectProperty: isChildOf
EquivalentTo: hasParent

We have no way of inferring the isSonOf and isDaughterOf from what already exists. What we want to happen is the implication of ‘Man and hasParent Person implies isSonOf’. OWL 2 and its reasoners cannot do this implication. It has been called the ‘man man problem’⁷. Solutions for this have been developed [3], but are not part of OWL 2 and its reasoners.

Figure 5.3: The property hierarchy for isChildOf and associated son/daughter properties

⁷ http://lists.w3.org/Archives/Public/public-owl-dev/2007JulSep/0177.html

Child	property	Parent
Robert David Bright 1965	isSonOf	David Bright 1934, Margaret Grace Rever 1934
Richard John Bright 1962	isSonOf	David Bright 1934, Margaret Grace Rever 1934
Mark Bright 1956	isSonOf	John Bright 1930, Joyce Gosport
Ian Bright 1959	isSonOf	John Bright 1930, Joyce Gosport
Janet Bright 1964	isDaughterOf	John Bright 1930, Joyce Gosport
William Bright 1970	isSonOf	John Bright 1930, Joyce Gosport

Table 5.1: Child property assertions for the FHKB

Thus we must resort to hand assertions of properties to test out our new path:

Task 20: Sons and daughters

Add the property hierarchy shown in Figure 5.3, together with the equivalent property axiom and the obvious inverses. As a test (after running the reasoner), ask the DL query isChildOf value David_Bright_1934 and you should have the answer of Richard and Robert; Add the sub-property paths as described in the text; Add the assertions shown in Table 5.1; Run the reasoner; Ask the DL query for the brother of Robert David Bright and the sister of Janet.

Of course, it works, but we see the same problem as above. As usual, think of the objects involved. Robert isSonOf David and David isParentOf Robert, so Robert is his own brother. Irreflexivity again causes problems as it does above (Task 18).

5.3 Siblings: Option two

Our option one has lots of problems. So, we have an option of asserting the various levels of sibling. We can take the same basic structure of sibling properties as before, but just fiddle around a bit and rely on more assertion while still trying to infer as much as possible. We will take the following approach:

• We will take off the sub-property chains of the sibling properties as they do not work;
• We will assert the leaf properties of the sibling sub-hierarchy sparsely and attempt to infer as much as possible.

Person	Property	Person
Robert David Bright 1965	isBrotherOf	Richard John Bright 1962
David Bright 1934	isBrotherOf	John Bright 1930
David Bright 1934	isBrotherOf	Peter William Bright 1941
Janet Bright 1964	isSisterOf	Mark Bright 1956
Janet Bright 1964	isSisterOf	Ian Bright 1959
Janet Bright 1964	isSisterOf	William Bright 1970
Mark Bright 1956	isBrotherOf	Ian Bright 1959
Mark Bright 1956	isBrotherOf	Janet Bright 1964
Mark Bright 1956	isBrotherOf	William Bright 1970

Table 5.2: The sibling relationships to add to the FHKB.

Do the following:

Task 21: Add sibling assertions

Remove the sub-property chains of the sibling properties and the isChildOf assertions as explained above. Add the Sibling assertions shown in table 5.2; Run the reasoner; Ask isBrotherOf value Robert_David_Bright_1965; Ask isBrotherOf value Richard_John_Bright_1962; Ask hasBrother value Robert_David_Bright_1965; Ask hasBrother value Richard_John_Bright_1962; Ask isSisterOf value William_Bright_1970; Ask the query Man and hasSibling value Robert_David_Bright_1965.

We can see some problems with this option as well:

• With these properties asserted, Richard only has a hasBrother property to Robert. We would really like an isBrotherOf to Robert to hold.
• The query Man and hasSibling value Robert only retrieves Robert himself. Because we only asserted that Robert is a brother of Richard, and the domain of isBrotherOf is Man we know that Robert is a Man, but we do not know anything about the Sex of Richard.

5.3.1 Which Modelling Option to Choose for Siblings?

Which of the two options gives the worse answers and which is the least effort? Option one is obviously the least effort; we only have to assert the same parentage facts as we already have; then the sub-property chains do the rest. It works OK for hasSibling, but we cannot do brothers and sisters adequately; we need Man and hasSibling ⊐ isBrotherOf and we cannot do that implication. This means we cannot ask the questions we need to ask.

So, we do option two, even though it is hard work and is still not perfect for query answering, even though we have gone for a sparse assertion mode. Doing full sibling assertion would work, but is a lot of effort.

We could start again and use the isSonOfandisDaughterOf option, with the sub-property chains described above. This still has the problem of everyone being their own sibling. It can get the sex specific sibling relationships, but requires a wholesale re-assertion of parentage facts. We will continue with option two, largely because it highlights some nice problems later on.

5.4 Half-Siblings

In Section 5.2 we briefly talked about half-siblings. So far, we have assumed full-siblings (or, rather, just talked about siblings and made no distinction). Ideally, we would like to accommodate distinctions between full- and half-siblings; here we use half-siblings, where only one parent is in common between two individuals, as the example. The short-answer is, unfortunately, that OWL 2 cannot deal with half-siblings in the way that we want - that is, such that we can infer properties between named individuals indicating full- or half-sibling relationships.

It is possible to find sets of half-brothers in the FHKB by writing a defined class or DL-query for a particular individual.} The following fragment of OWL defines a class that looks for the half-brothers of an individual called ‘Percival’:

Class: HalfBrotherOfPercival
EquivalentTo: Man and (((hasFather some (not (isFatherOf value Percival))) and
(hasMother some (isMotherOf value Percival))) or ((hasFather some (isFatherOf
value Percival)) and (hasMother some (not (isMotherOf value Percival)))))

Here we are asking for any man that either has Percival’s father but not his mother, or his mother, but not his father. This works fine, but is obviously not a general solution. The OWL description is quite complex and the writing will not scale as the number of options (hypothetically, as the number of parents increases... ) increases; it is fine for man/woman, but go any higher and it will become very tedious to write all the combinations.

Another way of doing this half-brother class to find the set of half-brothers of a individual is to use cardinality constraints:

Class: HalfBrotherOfPercival
EquivalentTo: Man and (hasParent exactly 1 (isParentOf value Percival))

This is more succinct. We are asking for a man that has exactly one parent from the class of individuals that are the class of Percival’s parents. This works, but one more constraint has to be present in the FHKB. We need to make sure that there can be only two parents (or indeed, just a specified number of parents for a person). If we leave it open as to the number of parents a person has, the reasoner cannot work out that there is a man that shares exactly one parent, as there may be other parents. We added this constraint to the FHKB in Section 6.2; try out the classes to check that they work.

These two solutions have been about finding sets of half-brothers for an individual. What we really want in the FHKB is to find half-brothers between any given pair of individuals.

Unfortunately we cannot, without rules, ask OWL 2 to distinguish full- and half-siblings – we cannot count the number of routes taken between siblings via different distinct intermediate parent objects.

5.5 Aunts and Uncles

An uncle is a brother of either my mother or father. An aunt is a sister of either my mother or father. In common practice, wives and husbands of aunts and uncles are usually uncles and aunts respectively. Formally, these aunts and uncles are aunts-in-law and uncles-in-law. Whatever approach we take, we cannot fully account for aunts and uncles until we have information about marriages, which will not have until Chapter 9. We will, however, do the first part now.

Look at the objects and properties between them for the following facts:

• Robert has father David and mother Margaret;
• David has brothers Peter and John;
• Margaret has a sister Eileen;
• Robert thus has the uncles John and Peter and an aunt Eileen.

As we are tracing paths or ‘chains’ of objects and properties we should use sub-property chains as a solution for the aunts and uncles. We can make an hasUncle property as follows (see Figure 5.4):

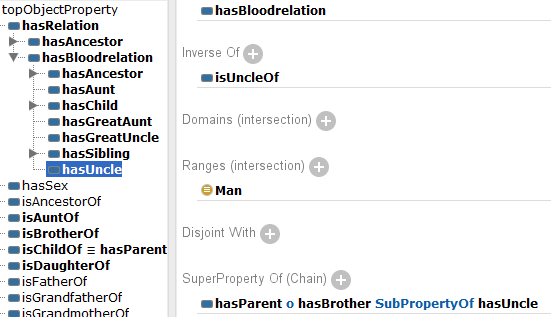
ObjectProperty: hasUncle
SubPropertyOf: hasBloodrelation
Domain: Man
Range: Person
SubPropertyChain: hasParent o hasBrother
InverseOf: isUncleOf

Figure 5.4: Tracing out the path between objects to get the hasUncle sub-property chain.

Notice we have the domain of Man and range of Person. We also have an inverse. As usual, we can read this as ‘an object that holds an hasParent property, followed by an object holding a hasBrother property, implies that the first object holds an hasUncle property with the last object’.

Note also where the properties (include the ones for aunt) go in the object property hierarchy. Aunts and uncles are not ancestors that are in the direct blood line of a person, but they are blood relations (in the narrower definition that we are using). Thus the aunt and uncle properties go under the hasBloodrelation property (see Figure 5.5). Again, think of the implications between objects holding a property between them; that two objects linked by a property implies that those two objects also hold all the property’s super-properties as well. As long as all the super-properties are true, the place in the object property hierarchy is correct (think about the implications going up, rather than down).

Figure 5.5: The object property hierarchy with the aunt and uncle properties included. On the right side, we can see the hasUncle property as shown by Protégé.

Do the following tasks:

Task 22: Uncles and Aunts
Add the hasUncle property as above; Add the hasAunt property as well; Ask for the uncles of Julie_Bright_1966 and for Mark_Bright_1956; Add similar properties for hasGreatUncle and hasGreatAunt and place them in the property hierarchy.

We can see this works – unless we have any gaps in the sibling relationships (you may have to fix these). Great aunts and uncles are simply a matter of adding another ‘parent’ leg into the sub-property chain. We are not really learning anything new with aunts and uncles, except that we keep gaining a lot for

free through sub-property chains. We just add a new property with its sub-property chain and we get a whole lot more inferences on individuals. To see what we now know about Robert David Bright, do the following:

Task 23: What do we know?
Save the ontology and run the reasoner; Look at inferences related to the individual Robert David Bright (see warning in the beginning of this chapter). If you chose to use DL queries in Protégé, do not forget to tick the appropriate check-boxes.

You can now see lots of facts about Robert David Bright, with only a very few actual assertions directly on Robert David Bright.

5.6 Summary

Siblings have revealed several things for us:

• We can use just the parentage facts to find siblings, but everyone ends up being their own sibling;
• We cannot make the properties irreflexive, as the knowledge base becomes inconsistent;
• We would like an implication of Man and hasSibling ⊃ isBrotherOf, but OWL 2 doesn’t do this implication;
• Whatever way we model siblings, we end up with a bit of a mess;
• OWL 2 cannot do half-siblings;
• However, we can get close enough and we can start inferring lots of facts via sub-property chains using the sibling relationships.

The FHKB ontology at this stage of the tutorial has an expressivity ofSRIF.

The time to reason with the FHKB at this point (in Protégé) on a typical desktop
machine by HermiT 1.3.8 is approximately 1355.614 sec (0.71682 % of final), by
Pellet 2.2.0 0.206 sec (0.00167 % of final) and by FaCT++ 1.6.4 is approximately
0.039 sec (0.001 % of final). 0 sec indicates failure or timeout.

Chapter 6

Individuals in Class Expressions

In this chapter you will:

1. Use individuals within class expressions;
2. Make classes to find Robert and Richard’s parents, ancestors, and so on;
3. Explore equivalence of such classes;
4. Re-visit the closed world.

Find a snapshot of the ontology at this stage below.

6.1 Richard and Robert’s Parents and Ancestors

So far we have only used object properties between unspecified objects. We can, however, specify a specific individual to act at the right-hand-side of a class restriction or type assertion on an individual. The basic syntax for so-called nominals is:

Class: ParentOfRobert
EquivalentTo: Person and isParentOf valueRobert_David_Bright_1965

This is an equivalence axiom that recognises any individual that is a Person and a parent of Robert David Bright.

Task 24: Robert and Richards parents

Create the class ParentOfRobert as described above; Classify – inspect where the class is placed in the FHKB TBox and look at which individuals classify as members of the class; Do the same for a class with the value of Richard_John_Bright_1962 and classify; Finally create a class ParentOfRichardAndRobert, defining it as Person and isParentOf some {Robert_David_Bright_1965 ,Richard_John_Bright_1962 }; again see what happens on classification. Note that the expressions isMotherOf value Robert_David_Bright_1965 and isMotherOf some {Robert_David_Bright_1965 } are practically identical. The only difference is that using value, you can only specify one individual, while some relates to a class (a set of individuals).

We see that these queries work and that we can create more complex nominal based class expressions. The disjunction above is

isParentOf some {Robert_David_Bright_1965, Richard_John_Bright_1965}

The ‘{’ and ‘}’ are a bit of syntax that says ‘here’s a class of individual’.

We also see that the classes for the parents of Robert David Bright and Richard John Bright have the same members according to the FHKB, but that the two classes are not inferred to be equivalent. Our domain knowledge indicates the two classes have the same extents (members) and thus the classes are equivalent, but the automated reasoner does not make this inference. As usual, this is because the FHKB has not given the automated reasoner enough information to make such an inference.

6.2 Closing Down What we Know About Parents and Siblings

The classes describing the parents of Richard and Robert are not equivalent, even though, as humans, we know their classes of parent are the same. We need more constraints so that it is known that the four parents are the only ones that exist. We can try this by closing down what we know about the immediate family of Robert David Bright.

In Chapter 4 we described that a Person has exactly one Woman and exactly one Man as mother and father (by saying that the hasMother and hasFather properties are functional and thus only one of each may be held by any one individual to distinct individuals). The parent properties are defined in terms of hasParent, hasMother and hasFather. The latter two imply hasParent. The two sub-properties are functional, but there are no constraints on hasParent, so an individual can hold many instances of this property. So, there is no information in the FHKB to say a Person has only two parents (we say there is one mother and one father, but not that there are only two parents). Thus Robert and Richard could have other parents and other grandparents than those in the FHKB; we have to close down our descriptions so that only two parents are possible. There are two ways of doing this:

1. Using qualified cardinality constraints in a class restriction;
2. Putting a covering axiom on hasParent in the same way as we did for Sex in Chapter 4.

Task 25: Closing the Person class
Add the restriction hasParent exactly 2 Person to the classPerson; Run the reasoner; Inspect the hierarchy to see where ParentOfRobert and ParentOfRichard are placed and whether or not they are found to be equivalent; Now add the restriction hasParent max 2 Person to the class Person; Run the reasoner (taking note of how long the reasoning takes) and take another look.

We find that these two classes are equivalent; we have supplied enough information to infer that these two classes are equivalent. So, we know that option one above works, but what about option two? This takes a bit of care to think through, but the basic thing is to think about how many ways there are to have a hasParent relationship between two individuals. We know that we can have either a hasFather or a hasMother property between two individuals; we also know that we can have only one of each of these properties between an individual and a distinct individual. However, the open world assumption tells us that there may be other ways of having a hasParent property between two individuals; we’ve not closed the possibilities. By putting on the hasParent exactly 2 Person restriction on the Person class, we are effectively closing down the options for ways that a person can have parents; we know because of the functional characteristic on hasMother and hasFather that we can have only one of each of these and the two restrictions say that one of each must exist. So, we know we have two ways of having a parent on each Person individual. So, when we say that there are exactly two parents (no more and no less) we have closed down the world of having parents—thus these two classes can be inferred to be equivalent. It is also worth noting that this extra axiom on the Person class will make the reasoner run much more slowly.

Finally, for option 2, we have no way of placing a covering axiom on a property. What we’d like to be able to state is something like:

ObjectProperty: hasParent
EquivalentTo: hasFather or hasMother

but we can’t.

6.3 Summary

For practice, do the following:

Task 26: Additional Practice
Add lots more classes using members of the ABox as nominals; Make complex expressions using nominals; After each addition of a nominal, classify and see what has been inferred within the FHKB. See if you can make classes for GrandparentOfRobert and GrandparentOfRichard and make them inferred to be equivalent.

In this chapter we have seen the use of individuals within class expressions. It allows us to make useful queries and class definitions. The main things to note is that it can be done and that there is some syntax involved. More importantly, some inferences may not be as expected due to the open world assumption in OWL.

By now you might have noticed a significant increase in the time the reasoner needs
to classify. Closing down what we know about family relationships takes its toll on
the reasoner performance, especially the usage of 'hasParent exactly 2 Person'. At
this point we recommend rewriting this axiom to 'hasParent max 2 Person'. It gives
us most of what we need, but has a little less negative impact on the reasoning
time.

The FHKB ontology at this stage of the tutorial has an expressivity of SROIQ.

The time to reason with the FHKB at this point (in Protégé) on a typical desktop
machine by HermiT 1.3.8 is approximately 2067.273 sec (1.09313 % of final), by
Pellet 2.2.0 0.529 sec (0.00428 % of final) and by FaCT++ 1.6.4 is approximately
0.147 sec (0.004 % of final). 0 sec indicates failure or timeout.

Chapter 7

Data Properties in the FHKB

We now have some individuals with some basic object properties between individuals. OWL 2, however, also has data properties that can relate an object or individual to some item of data. There are data about a Person, such as years of events and names etc. So, in this Chapter you will:

1. Make some data properties to describe event years to people;
2. Create some simple defined classes that group people by when they were born;
3. Try counting the numbers of children people have...
4. Deal with the open world assumption;
5. Add given and family names to individuals in the FHKB.

Find a snapshot of the ontology at this stage below.

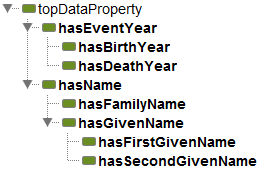
7.1 Adding Some Data Properties for Event Years

Everyone has a birth year; death year; and some have a marriage year and so on. We can model these simply with data properties and an integer as a filler. OWL 2 has a DateTime datatype, where it is possible to specify a precise time and date down to a second. ⁷ This proves cumbersome (see http://robertdavidstevens.wordpress.com/2011/05/05/using-the-datetime-data-type-to-describe-birthdays/ for details); all we need is a simple indication of the year in which a person was born. Of course, the integer type has a zero, which the Gregorian calendar for which we use integer as a proxy does not, but integer is sufficient to our needs. Also, there are various ontological treatments of time and information about people (this extends to names etc. as well), but we gloss over that here—that’s another tutorial.

⁷ http://www.w3.org/TR/2008/WD-owl2-quick-reference-20081202/#Built-in_Datatypes_and_Facets

We can have dates for birth, death and (eventually) marriage (see Chapter 9) and we can just think of these as event years. We can make a little hierarchy of event years as shown in Figure 7.1).

Task 27: Create a data property hierarchy

Create the data property hasEventYear with range integer and domain Person; Create the data property hasBirthYear and make it a sub-property of hasEventYear (that way, the domain and range of hasEventYear are inherited); Create the data property hasDeathYear and make it a sub-property of hasEventYear; For each individual add the birth years shown in Table A.1 (see appendix). You do not actually have to go back to the table—it is easier to read the birth years simply off the individual names.

Again, asserting birth years for all individuals can be a bit tedious. Find a snapshot of the ontology at this stage below.

We now have an ABox with individuals with fact assertions to data indicating a birth year. We can, if we wish, also add a class restriction to the Person class saying that each and every instance of the class Person holds a data property to an integer and that this property is called ‘hasBirthYear’. As usual when deciding whether to place such a restriction upon a class, ask whether it is true that each and every instance of the class holds that property; this is exactly the same as we did for the object properties in Chapter 4. Everyone does have a birth year, even if it is not known.

Once birth years have been added to our individuals, we can start asking some questions.

Task 28: DL queries
1. Use a DL query to ask: Person born after 1960; Person born in the 1960s; Person born in the 1800s; Person that has fewer than three children; Person that has more than three children.

The DL query for people born in the 1960s is:

Person and hasBirthYear some int[>= 1960, < 1970]

This kind of interval is known as a facet.

7.1.1 Counting Numbers of Children

The last two queries in the list do not work as expected. We have asked, for instance, for Person that have more than three children, but we get no members of Person in the answer, though we know that there are some in the FHKB (e.g., John_Bright_1930). This is because there is not enough information in the FHKB to tell that this person has more than three different people as children. As humans we can look at the four children of John Bright and know that they are different – for instance, they all have different birth years. The automated reasoner, however, does not know that a Person can only have one birth year.

Task 29: Make a functional object property
Make the property hasBirthYear functional. Ask the query for Person that has more than three children again.

This time the query should work. All the other event year properties should be made functional, expect hasEventYear, as one individual can have many event years. As the children have different birth year and an individual can only hold one hasBirthYear property, then these people must be distinct entities.

Of course, making birth year functional is not a reliable way of ensuring that the automated reasoner knows that the individual are different. It is possible for two Person to have the same birth year within the same family – twins and so on. Peter_William_Bright_1941 has three children, two of which are twins, so will not be a member of the class of people with at least three children. So, we use the different individuals axiom. Most tools, including Protégé, have a feature that allows all individuals to be made different.

Task 30: Make all individuals different
Make all individuals different; Ask the above queries again.

From now on, every time you add individuals, make sure the different individuals axiom is updated.

7.2 The Open World Assumption

We have met again the open world assumption and its importance in the FHKB. In the use of the functional characteristic on the hasBirthYear property, we saw one way of constraining the interpretation of numbers of children. We also introduced the ‘different individuals’ axiom as a way of making all individuals in a knowledge base distinct. There are more questions, however, for which we need more ways of closing down the openness of OWL 2.

Take the questions:

• People that have exactly two children;
• People that have only brothers;
• People that have only female children.

We can only answer these questions if we locally close the world.We have said that David and Margaret have two children, Richard and Robert, but we have not said that there are not any others. As usual, try not to apply your domain knowledge too much; ask yourself what the automated reasoner actually knows. As we have the open world assumption, the reasoner will assume, unless otherwise said, that there could be more children; it simply doesn’t know.

Think of a railway journey enquiry system. If I ask a standard closed world system about the possible routes by rail, between Manchester and Buenos Aires, the answer will be ’none’, as there are none described in the system. With the open world assumption, if there is no information in the system then the answer to the same question will simply be ‘I don’t know’. We have to explicitly say that there is no railway route from Manchester to Buenos Aires for the right answer to come back.

We have to do the same thing in OWL. We have to say that David and Margaret have only two children. We do this with a type assertion on individuals. So far we have only used fact assertions. A type assertion to close down David Bright’ parentage looks like this:

isParentOf only {Robert_David_Bright_1965,Richard_John_Bright_1962 }

This has the same meaning as the closure axioms that you should be familiar with on classes. We are saying that the only fillers that can appear on the right-hand-side of the isParentOf property on this individual are the two individuals for Richard and Robert. We use the braces to represent the set of these two individuals.

Task 31: Make a closure axiom
Add the closure assertion above to David Bright; Issue the DL query isParentOf exactly 2 Person.

The last query should return the answer of David Bright. Closing down the whole FHKB ABox is a chore and would really have to be done programmatically. OWL scripting languages such as the Ontology Preprocessing Language⁸ (OPPL) [2] can help here. Also going directly to the OWL API [1]⁹, if you know what you are doing, is another route.

Adding all these closure type assertions can slow down the reasoner; so think about
the needs of your system – just adding it ‘because it is right’ is not necessarily the
right route.

⁸ http://oppl2.sourceforge.net

⁹ http://owlapi.sourceforge.net/

7.3 Adding Given and Family Names

We also want to add some other useful data facts to people – their names. We have been putting names as part of labels on individuals, but data fact assertions make sense to separate out family and given names so that we can ask questions such as ‘give me all people with the family name Bright and the first given name of either James or William’. A person’s name is a fact about that person and is more, in this case, than just a label of the representation of that person. So, we want family names and given names. A person may have more than one given name – ‘Robert David’, for instance – and an arbitrary number of given names can be held. For the FHKB, we have simply created two data properties of hasFirstGivenName and hasSecondGivenName). Ideally, it would be good to have some index on the property to given name position, but OWL has no n-ary relationships. Otherwise, we could reify the hasGivenName property into a class of objects, such as the following:

Class: GivenName
SubClassOf:hasValue some String,
hasPosition some Integer

but it is really rather too much trouble for the resulting query potential.

As already shown, we will use data properties relating instances of Person to strings. We want to distinguish family and given names, and then different positions of given names through simple conflating of position into the property name. Figure 7.1 shows the intended data property hierarchy.

Figure 7.1: The event year and name data property hierarchies in the FHKB.

Do the following:

Task 32: Data properties

Create the data properties as described in Figure 7.1; Give the hasName property the domain of Person and the range of String; Make the leaf properties of given names functional; Add the names shown in Table A.1 (appendix); Again, it may be easier to read the names of the individual names. Ask the questions: all the people with the first given name ‘James’; all the people with the first given name ‘William’; All the people with the given name ‘William’; All the people with the given name ‘William’ and the family name ‘Bright’.

The name data property hierarchy and the queries using those properties displays what now should be familiar. Sub-properties that imply the super-property. So, when we ask hasFirstGivenName value "William" and then the query hasGivenName value value "William" we can expect different answers. There are people with ‘William’ as either first or second given name and asking the question with the super-property for given names will collect both first and second given names.

7.4 Summary

We have used data properties that link objects to data such as string, integer, floats and Booleans etc. OWL uses the XML data types. We have seen a simple use of data properties to simulate birth years. The full FHKB also uses them to place names (given and family) on individuals as strings. This means one can ask for the Person with the given name "James", of which there are many in the FHKB.

Most importantly we have re-visited the open world assumption and its implications for querying an OWL ABox. We have looked at ways in which the ABox can be closed down – unreliably via the functional characteristic (in this particular case) and more generally via type assertions.

All the DL queries used in this chapter can also serve as defined classes in the TBox. It is a useful exercise to progressively add more defined classes to the FHKB TBox. Make more complex queries, make them into defined classes and inspect where they appear in the class hierarchy.

The FHKB ontology at this stage of the tutorial has an expressivity of SROIQ(D).

The time to reason with the FHKB at this point (in Protégé) on a typical desktop
machine by HermiT 1.3.8 is approximately 1891.157 sec (1.00000 % of final), by
Pellet 2.2.0 1.134 sec (0.00917 % of final) and by FaCT++ 1.6.4 is approximately
0.201 sec (0.006 % of final). 0 sec indicates failure or timeout.

Note that we now cover the whole range of expressivity of OWL 2. HermiT at
least is impossibly slow by now. This may be because HermiT does more work
than the others. For now, we recommend to use either Pellet or FaCT++.

Chapter 8

Cousins in the FHKB

In this Chapter you will

1. Revise or get to know about degrees and removes of cousin;
2. Add the properties and sub-property chains for first and second cousins;
3. Add properties and sub-property chains for some removes of cousins;
4. Find out that the siblings debacle haunts us still;
5. Add a defined class that does first cousins properly.

Find a snapshot of the ontology at this stage below.

Be warned; from here on the reasoner can start running slowly! Please see warning
at the beginning of the last chapter for more information.

8.1 Introducing Cousins

Cousins can be confusing, but here is a brief summary:

• First cousins share a grandparent, but are not siblings;
• Second cousins share a great grandparent, but are not first cousins or siblings;
• Degrees such as first and second cousin give the distance to the nearest common ancestor;
• Removes give differences in generation. So, my Dad’s first cousins (his generation) are my (Robert David Bright’s) first cousins once removed.

Simply, my first cousins are my parent’s sibling’s children. As usual, we can think about the objects and put in place some sub-property chains.

8.2 First Cousins

Figure 8.1: Tracing out the sub-property chain for cousins going from a child to a parent, to its sibling, and down to its child, a cousin

Figure 8.1 shows the sub-property chain for first cousins. As usual, think at the object level; to get to the first cousins of Robert David Bright, we go to the parents of Robert David Bright, to their siblings and then to their children. We go up, along and down. The OWL for this could be:

ObjectProperty: hasFirstCousin
SubPropertyOf: hasCousin
SubPropertyChain: hasParent o hasSibling o hasChild
Characteristics: Symmetric

Note that we follow the definitions in Section 8.1 of first cousins sharing a grandparent, but not a parent. The sub-property chain goes up to children of a grandparent (a given person’s parents), along to siblings and down to their children. We do not want this property to be transitive. One’s cousins are not necessarily my cousins. The blood uncles of Robert David Bright have children that are his cousins. These first cousins, however, also have a mother that is not a blood relation of Robert David Bright and the mother’s sibling’s children are not cousins of Robert David Bright.

We do, however, want the property to be symmetric. One’s cousins have one’s-self as a cousin.

We need to place the cousin properties in the growing object property hierarchy. Cousins are obviously blood relations, but not ancestors, so they go off to one side, underneath hasBloodrelation. We should group the different removes and degree of cousin underneath one hasCousin property and this we will do.

Do the following:

Task 33: First cousins
Add the property of hasCousin to the hierarchy underneath hasBloodrelation; Add hasFirstCousin underneath this property; Add the sub-property chain as described above; Run the reasoner and look at the first cousins of Robert David Bright.

You should see the following people as first cousins of Robert David Bright: Mark Anthony Heath, Nicholas Charles Heath, Mark Bright, Ian Bright, Janet Bright, William Bright, James Bright, Julie Bright, Clare Bright, Richard John Bright and Robert David Bright. The last two, as should be expected, are first cousins of Robert David Bright and this is not correct. As David Bright will be his own brother, his children are his own nieces and nephews and thus the cousins of his own children. Our inability to infer siblings correctly in the FHKB haunts us still and will continue to do so.

Although the last query for the cousins of Robert David Bright should return the
same results for every reasoner, we have had experiences where the results differ.

8.3 Other Degrees and Removes of Cousin

Other degrees of cousins follow the same pattern as for first cousins; we go up, along and down. For second cousins we go up from a given individual to children of a great grandparent, along to their siblings and down to their grandchildren. The following object property declaration is for second cousins (note it uses the isGrandparentOf and its inverse properties, though the parent properties could be used) :

ObjectProperty: hasSecondCousin
SubPropertyOf: hasCousin
SubPropertyChain: hasGrandParent o hasSibling o isGrandParentOf
Characteristics: Symmetric

‘ Removes ’ simply add in another ‘leg’ of either ‘up’ or ‘down’ either side of the ‘along’—that is, think of the actual individuals involved and draw a little picture of blobs and lines—then trace your finger up, along and down to work out the sub-property chain. The following object property declaration does it for first cousins once removed (note that this has been done by putting this extra ‘leg’ on to the hasFirstCousin property; the symmetry of the property makes it work either way around so that a given person is the first cousin once removed of his/her first cousins once removed):

ObjectProperty: hasFirstCousinOnceRemoved
SubPropertyOf: hasCousin
SubPropertyChain: hasFirstCousin o hasChild
Characteristics: Symmetric

To exercise the cousin properties do the following:

Task 34: Cousin properties
Add properties for second degree cousins; Add removes for first and second degree cousins; Run the reasoner and check what we know about Robert David Bright’ other types of cousin.

You should see that we see some peculiar inferences about Robert David Bright’ cousins – not only are his brother and himself his own cousins, but so are his father, mother, uncles and so on. This makes sense if we look at the general sibling problem, but also it helps to just trace the paths around. If we go up from one of Robert David Bright’ true first cousins to a grandparent and down one parent relationship, we follow the first cousin once removed path and get to one of Robert David Bright’ parents or uncles. This is not to be expected and we need a tighter definition that goes beyond sub-property chains so that we can exclude some implications from the FHKB.

8.4 Doing First Cousins Properly

As far as inferring first cousin facts for Robert David Bright, we have failed. More precisely, we have recalled all Robert David Bright’s cousins, but the precision is not what we would desire. What we can do is ask for Robert David Bright’ cousins, but then remove the children of Robert David Bright’ parents. The following DL query achieves this:

Person that hasFirstCousin valueRobert_David_Bright_1965
and (not (hasFather valueDavid_Bright_1934) or not (hasMother valueMar-
garet_Grace_Rever_1934)

This works, but only for a named individual. We could make a defined class for this query; we could also make a defined class FirstCousin, but it is not of much utility. We would have to make sure that people whose parents are not known to have siblings with children are excluded. That is, people are not ‘first cousins’ whose only first cousins are themselves and their siblings. The following class does this:

Class: FirstCousin
EquivalentTo: Person that hasFirstCousin some Person

Task 35: Roberts first cousins
Make a defined class FirstCousin as shown above; Make a defined class FirstCousinOfRobert; Create a DL query that looks at Robert_David_Bright_1965 first cousins and takes away the children of Robert_David_Bright_1965’ parents as shown above.

This gives some practice with negation. One is making a class and then ‘taking’ some of it away – ‘these, but not those’.

8.5 Summary

We have now expanded the FHKB to include most blood relationships. We have also found that cousins are hard to capture just using object properties and sub-property chains. Our broken sibling inferences mean that we have too many cousins inferred at the instance level. We can get cousins right at the class level by using our inference based cousins, then excluding some using negation. Perhaps not neat, but it works.

We have reinforced that we can just add more and more relationships to individuals by just adding more properties to our FHKB object property hierarchy and adding more sub-property chains that use the object properties we have built up upon parentage and sibling properties; this is as it should be.

The FHKB ontology at this stage of the tutorial has an expressivity of SROIQ(D).

The time to reason with the FHKB at this point (in Protégé) on a typical desktop
machine by HermiT 1.3.8 is approximately 0.000 sec (0.00000 % of final), by Pellet
2.2.0 111.395 sec (0.90085 % of final) and by FaCT++ 1.6.4 is approximately 0.868
sec (0.024 % of final). 0 sec indicates failure or timeout.

Chapter 9

Marriage in the FHKB

In this chapter you will:

1. Model marriages and relationships;
2. Establish object properties for husbands, wives and various in-laws;
3. Re-visit aunts and uncles to do them properly;
4. Use more than one sub-property chain on a given property.

Find a snapshot of the ontology at this stage below.

Much of what is in this chapter is really revision; it is more of the same - making
lots of properties and using lots of sub-property chains. However, it is worth it as
it will test your growing skills and it also makes the reasoners and yourself work
hard. There are also some good questions to ask of the FHKB as a result of adding
marriages.

9.1 Marriage

Marriage is a culturally complex situation to model. The FHKB started with a conservative model of a marriage involving only one man and one woman.¹⁰ Later versions are more permissive; a marriage simply has a minimum of two partners. This leaves it open to numbers and sex of the people involved. In fact, ‘marriage’ is probably not the right name for it. Using BreedingRelationship as a label (the one favoured by the main author’s mother) may be a little too stark and might be a little exclusive.... In any case, some more generic name is probably better and various subclasses of the FHKB’s Marriage class are probably necessary.

¹⁰ There being no funny stuff in the Stevens family.

To model marriage do the following:

Task 36: Marriage

Create a class Marriage, subclass of DomainEntity; Create the properties: hasPartner(domain Marriage and range Person) and isPartnerIn hasFemalePartner(domain Marriage and range Woman, sub-property of hasPartner) and its inverse isFemalePartnerIn; a sub-property of hasPartner has MalePartner (domain Marriage and range Man)and its inverse isMalePartnerIn; Create the data property hasMarriageYear, making us a sub-property of hasEventYear,make it functional; Create an individual m001 with the label Marriage of David and Margaret and add the facts: hasMalePartner David_Bright_1934; hasFemalePartner Margaret_Grace_Rever_1934 hasMarriageYear 1958; Create an individual m002 with the label Marriage of John and Joyce and add the facts: hasMalePartner John_Bright_1930; hasFemalePartner Joyce_Gosport(you may have to add Joyce if you did not already did that); hasMarriageYear 1955; Create an individual m003 with the label Marriage of Peter and Diana and add the facts: hasMalePartner Peter_William_Bright_1941; hasFemalePartner Diana_Pool(you may have to add Diana if you did not already did that); hasMarriageYear 1964;

We have the basic infrastructure for marriages. We can ask the usual kinds of questions; try the following:

Task 37: DL queries
Ask the following DL queries: The Women partners in marriages; Marriages that happened before 1960 (see example below); Marriages that happened after 1960; Marriages that involved a man with the family name ‘Bright’.

DL query: Marriage and hasMarriageYear some int[<= 1960]

9.1.1 Spouses

This marriage infrastructure can be used to infer some slightly more interesting things for actual people. While we want marriage objects so that we can talk about marriage years and even locations, should we want to, we also want to be able to have the straight-forward spouse relationships one would expect. We can use sub-property chains in the usual manner; do the following:

Task 38: Wifes and Husbands
Create a property hasSpouse with two sub-properties hasHusband and hasWife. Create the inverses isSpouseOf, isWifeOf and isHusbandOf. To the hasWife property, add the sub-property chain isMalePartnerIn o hasFemalePartner. Follow the same pattern for the hasHusband property.

Figure 9.1 shows what is happening with the sub-property chains. Note that the domains and ranges of the spouse properties come from the elements of the sub-property chains. Note also that the hasSpouse relationship will be implied from its sub-property chains.

The following questions can now be asked:

• Is wife of David Bright;
• Has a husband born before 1940;
• The wife of an uncle of William Bright 1970.

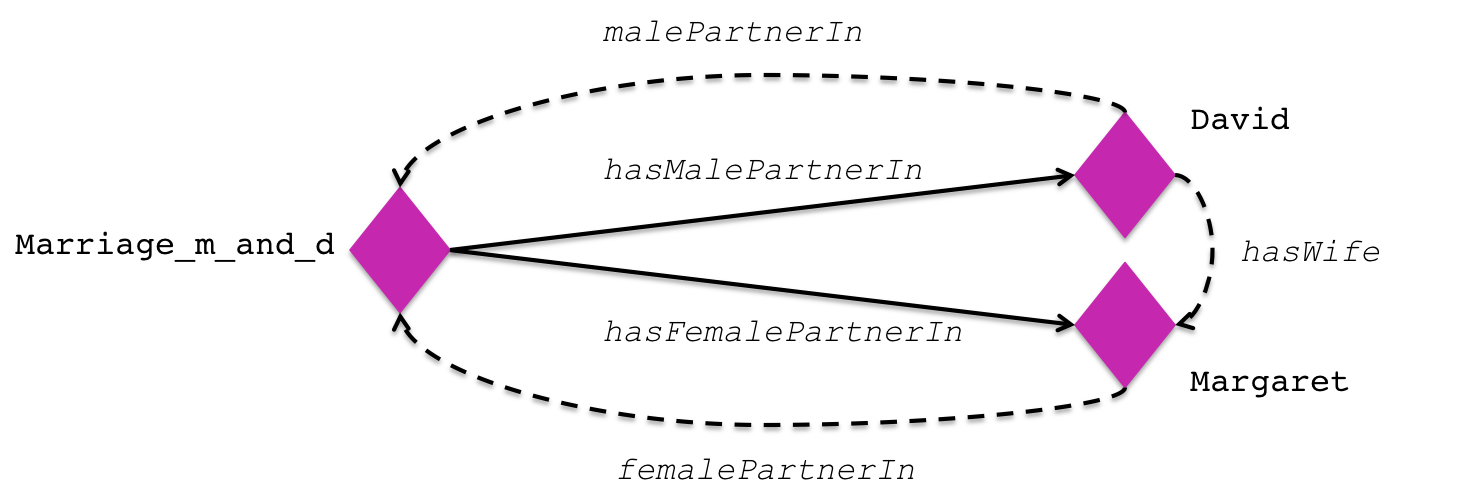
Figure 9.1: The sub-property chain path used to infer the spouse relationships via the marriage partnerships.

and many more. This is really a chance to explore your querying abilities and make some complex nested queries that involve going up and down the hierarchy and tracing routes through the graph of relationships between the individuals you’ve inferred.

9.2 In-Laws

Now we have spouses, we can also have in-laws. The path is simple: isSpouseOf o hasMother implies hasMotherInLaw. The path involved in mother-in-laws can be seen in Figure 9.2. The following OWL code establishes the sub-property chains for hasMotherInLaw:

ObjectProperty: hasMotherInLaw
SubPropertyOf: hasParentInLaw
SubPropertyChain: isSpouseOf o hasMother
Domain: Person
Range: Woman
InverseOf: isMotherInLawOf

Figure 9.2: Tracing out the path between objects to make the sub-property chain for mother-in-laws

Do the following to make the parent in-law properties:

Task 39: Parents in-law
Create hasParentInLaw with two sub-properties of hasMotherInLaw and hasFatherInLaw; Create the inverses, but remember to let the reasoner infer the hierarchy on that side of the hierarchy; Add the sub-property chains as described in the pattern for hasMotherInLaw above; Run the reasoner and check that the mother-in-law of Margaret Grace Rever is Iris Ellen Archer.

9.3 Brothers and Sisters In-Law

Brothers and sisters in law have the interesting addition of having more than one path between objects to establish a sister or brother in law relationship. The OWL code below establishes the relationships for ‘is sister in law of’:

ObjectProperty: hasSisterInLaw
SubPropertyOf: hasSiblingInLaw
SubPropertyChain: hasSpouse o hasSister
SubPropertyChain: hasSibling o isWifeOf

A wife’s husband’s sister is a sister in law of the wife. Figure 9.3 shows the two routes to being a sister-in-law. In addition, the wife is a sister in law of the husband’s siblings. One can add as many sub-property chains to a property as one needs. You should add the properties for hasSiblingInLawOf and its obvious sub-properties following the inverse of the pattern above.

Task 40: Siblings in-law
Create the relationships for siblings-in-law as indicated in the owl code above.

By now, chances are high that the realisation takes a long time. We recommend to
remove the very computationally expensive restriction `hasParent` exactly 2 Person
on the `Person` class, if you have not done it so far.

Figure 9.3: The two routes to being a sister-in-law.

9.4 Aunts and Uncles in-Law

The uncle of Robert David Bright has a wife, but she is not the aunt of Robert David Bright, she is the aunt-in-law. This is another kith relationship, not a kin relationship. The pattern has a familiar feel:

ObjectProperty: isAuntInLawOf
SubPropertyOf: isInLawOf
SubPropertyChain: isWifeOf o isBrotherOf o isParentOf

Task 41: Uncles and aunts in-law

Create hasAuntInLaw and hasUncleInLaw in the usual way; Test in the usual way; Tidy up the top of the property hierarchy so that it looks like Figure 9.4. We have a top property of hasRelation and two sub-properties of isBloodRelationOf and isInLawOf to establish the kith and kin relationships respectively; All the properties created in this chapter (except for spouses) should be underneath isInLawOf.

Figure 9.4: The object property hierarchy after adding the various in-law properties.

9.5 Summary

This has really been a revision chapter; nothing new has really been introduced. We have added a lot of new object properties and one new data property. The latest object property hierarchy with the ‘in-law’ branch can be seen in Figure 9.4. Highlights have been:

• Having an explicit marriage object so that we can say things about the marriage itself, not just the people in the marriage;
• We have seen that more than one property chain can be added to a property;
• We have added a lot of kith relationships to join the kin or blood relationships;
• As usual, the reasoner can establish the hierarchy for the inverses and put a lot of the domain and ranges in for free.

The FHKB ontology at this stage of the tutorial has an expressivity of SROIQ(D).

The time to reason with the FHKB at this point (in Protégé) on a typical desktop
machine by HermiT 1.3.8 is approximately 0.000 sec (0.00000 % of final), by Pellet
2.2.0 123.655 sec (1.00000 % of final) and by FaCT++ 1.6.4 is approximately 1.618
sec (0.046 % of final). 0 sec indicates failure or timeout.

Chapter 10

Extending the TBox

In this chapter you will:

1. Just add lots of defined classes for all the aspects we have covered in this FHKB tutorial;
2. You will learn that the properties used in these defined classes must be chosen with care.

Find a snapshot of the ontology at this stage below.

10.1 Adding Defined Classes

Add the following defined classes:

Task 42: Adding defined classes

Relation and blood relation; Forefather and Foremother; Grandparent, Grandfather and Grandmother; GreatGrandparent, GreatGrandfather and GreatGrandmother; GreatGrandparentOfRobert, GreatGrandfatherOfRobert and GreatGrandMotherOfRobert Daughter, Son, Brother, Sister, Child; Aunt, Uncle, AuntInLaw, UncleInLaw, GreatAunt and GreatUncle; FirstCousin and SecondCousin; First cousin once removed; InLaw, MotherInLaw, FatherInLaw, ParentInLaw, SiblingInLaw, SisterInLaw, BrotherInLaw; Any defined class for any property in the hierarchy and any nominal variant of these classes.

The three classes of Child, Son and Daughter are of note. They are coded in the following way:

Class: Child EquivalentTo: Person that hasParent Some Person
Class: Son EquivalentTo: Man that hasParent Some Person
Class: Daughter EquivalentTo: Woman that hasParent Some Person

After running the reasoner, you will find that Person is found to be equivalent to Child; Daughter is equivalent to Woman and that Son is equivalent to Man. This does, of course, make sense – each and every person is someone’s child, each and every woman is someone’s daughter. We will forget evolutionary time-scales where this might be thought to break down at some point – all Person individuals are also Descendant individuals, but do we expect some molecule in some prebiotic soup to be a member of this class?

Nevertheless, within the scope of the FHKB, such inferred equivalences are not unreasonable. They are also instructive; it is possible to have different intentional descriptions of a class and for them to have the same logical extents. You can see another example of this happening in the amino acids ontology, but for different reasons.

Taking Grandparent as an example class, there are two ways of writing the defined class:

Class: Grandparent EquivalentTo: Person and isGrandparentOf some Person
Class: Grandparent EquivalentTo: Person and (isParentOf some (Person and (is-
ParentOf some Person))

Each comes out at a different place in the class hierarchy. They both capture the right individuals as members (that is, those individuals in the ABox that are holding a isGrandparentOf property), but the class hierarchy is not correct. By definition, all grandparents are also parents, but the way the object property hierarchy works means that the first way of writing the defined class (with the isGrandparentOf property) is not subsumed by the class Parent. We want this to happen in any sensible class hierarchy, so we have to use the second pattern for all the classes, spelling out the sub-property path that implies the property such as isGrandparentOf within the equivalence axiom.

The reason for this need for the ‘long-form’ is that the isGrandparentOf does not imply the isParentOf property. As described in Chapter 3 if this implication were the case, being a grandparent of Robert David Bright, for instance, would also imply that the same Person were a parent of Robert David Bright; an implication we do not want. As these two properties (isParentOf and isGrandparentOf) do not subsume each other means that the defined classes written according to pattern one above will not subsume each other in the class hierarchy. Thus we use the second pattern. If we look at the class for grandparents of Robert:

Class: GrandparentOfRobert
EquivalentTo: Person that isParentOf some (Person that isParentOf value Robert
David Bright)

If we make the equivalent class for Richard John Bright, apply the reasoner and look at the hierarchy, we see that the two classes are not logically equivalent, even though they have the same extents of William George Bright, Iris Ellen Archer, Charles Herbert Rever and Violet Sylvia Steward. We looked at this example in Section 6.2, where there is an explanation and solutions.

10.2 Summary

We can add defined classes based on each property we have put into the object property hierarchy. We see the expected hierarchy; as can be seen from Figure 10.1 it has an obvious symmetry based on sex. We also see a lot of equivalences inferred – all women are daughters, as well as women descendants. Perhaps not the greatest insight ever gained, but it at least makes sense; all women must be daughters. It is instructive to use the explanation feature in Protégé to look at why the reasoner has made these inferences. For example, take a look at the class hasGrandmother some Woman – it is instructive to see how many there are.

Like the Chapter on marriage and in-law (Chapter 9), this chapter has largely been revision. One thing of note is, however, that we must not use the object properties that are inferred through sub-property chains as definitions in the TBox; we must spell out the sub-property chain in the definition, otherwise the implications do not work properly.

One thing is almost certain; the resulting TBox is rather complex and would be almost impossible to maintain by hand.

Figure 10.1: The full TBox hierarchy of the FHKB

The FHKB ontology at this stage of the tutorial has an expressivity of SROIQ(D).

The time to reason with the FHKB at this point (in Protégé) on a typical desktop
machine by HermiT 1.3.8 is approximately 0.000 sec (0.00000 % of final), by Pellet
2.2.0 0.000 sec (0.00000 % of final) and by FaCT++ 1.6.4 is approximately 35.438
sec (1.000 % of final). 0 sec indicates failure or timeout.

Chapter 11

Final remarks

If you have done all the tasks within this tutorial, then you will have touched most parts of OWL 2. Unusually for most uses of OWL we have concentrated on individuals, rather than just on the TBox. One note of warning – the full FHKB has some 450 members of the Bright family and takes a reasonably long time to classify, even on a sensible machine. The FHKB is not scalable in its current form.

One reason for this is that we have deliberately maximised inference. We have attempted not to explicitly type the individuals, but drive that through domain and range constraints. We are making the property hierarchy do lots of work. For the individual Robert David Bright, we only have a couple of assertions, but we infer some 1 500 facts between Robert David Bright and other named individuals in the FHKB–displaying this in Protégé causes problems. We have various complex classes in the TBox and so on.

We probably do not wish to drive a genealogical application using an FHKB in this form. Its purpose is educational. It touches most of OWL 2 and shows a lot of what it can do, but also a considerable amount of what it cannot do. As inference is maximised, the FHKB breaks most of the OWL 2 reasoners at the time of writing.However, it serves its role to teach about OWL 2.

OWL 2 on its own and using it in this style, really does not work for family history. We have seen that siblings and cousins cause problems. rules in various forms can do this kind of thing easily—it is one of the primary examples for learning about Prolog. Nevertheless, the FHKB does show how much inference between named individuals can be driven from a few fact assertions and a property hierarchy. Assuming a powerful enough reasoner and the ability to deal with many individuals, it would be possible to make a family history application using the FHKB; as long as one hid the long and sometimes complex queries and manipulations that would be necessary to ‘prune’ some of the ‘extra’ facts found about individuals. However, the FHKB does usefully show the power of OWL 2, touch a great deal of the language and demonstrate some of its limitations.

Appendix A

FHKB Family Data

Table A.1: The list of individuals in the FHKB

Person	First given name	Second given name	Family name	Birth year	Mother	Father
Alec John Archer 1927	Alec	John	Archer	1927	Violet Heath 1887	James Alexander Archer 1882
Charles Herbert Rever 1895	Charles	Herbert	Rever	1895	Elizabeth Frances Jessop 1869	William Rever 1870
Charlotte Caroline Jane Bright 1894	Charlotte	Caroline Jane	Bright	1894	Charlotte Hewett 1863	Henry Edmund Bright 1862
Charlotte Hewett 1863	Charlotte	none	Hewett	1863	not specified	not specified
Clare Bright 1966	Clare	none	Bright	1966	Diana Pool	Peter William Bright 1941
Diana Pool	Diana	none	Pool	none	not specified	not specified
David Bright 1934	David	none	Bright	1934	Iris Ellen Archer 1906	William George Bright 1901
Dereck Heath	Dereck	none	Heath	1927	not specified	not specified
Eileen Mary Rever 1929	Eileen	Mary	Rever	1929	Violet Sylvia Steward 1894	Charles Herbert Rever 1895
Elizabeth Frances Jessop 1869	Elizabeth	Frances	Jessop	1869	not specified	not specified
Ethel Archer 1912	Ethel	none	Archer	1912	Violet Heath 1887	James Alexander Archer 1882
Frederick Herbert Bright 1889	Frederick	Herbert	Bright	1889	Charlotte Hewett 1863	Henry Edmund Bright 1862
Henry Edmund Bright 1862	Henry	Edmund	Bright	1862	not specified	not specified
Henry Edmund Bright 1887	Henry	Edmund	Bright	1887	Charlotte Hewett 1863	Henry Edmund Bright 1862
Ian Bright 1959	Ian	none	Bright	1959	Joyce Gosport	John Bright 1930
Iris Ellen Archer 1906	Iris	Ellen	Archer	1906	Violet Heath 1887	James Alexander Archer 1882
James Alexander Archer 1882	James	Alexander	Archer	1882	not specified	not specified
James Bright 1964	James	none	Bright	1964	Diana Pool	Peter William Bright 1941
James Frank Hayden Bright 1891	James	Frank	Bright	1891	Charlotte Hewett 1863	Henry Edmund Bright 1862
Janet Bright 1964	Janet	none	Bright	1964	Joyce Gosport	John Bright 1930
John Bright 1930	John	none	Bright	1930	Iris Ellen Archer 1906	William George Bright 1901
John Tacey Steward 1873	John	Tacey	Steward	1873	not specified	not specified
Joyce Archer 1921	Joyce	none	Archer	1921	Violet Heath 1887	James Alexander Archer 1882
Joyce Gosport	Joyce	none	Gosport	not specified	not specified	not specified
Julie Bright 1966	Julie	none	Bright	1966	Diana Pool	Peter William Bright 1941
Kathleen Minnie Bright 1904	Kathleen	Minnie	Bright	1904	Charlotte Hewett 1863	Henry Edmund Bright 1862
Leonard John Bright 1890	Leonard	John	Bright	1890	Charlotte Hewett 1863	Henry Edmund Bright 1862
Lois Green 1871	Lois	none	Green	1871	not specified	not specified
Margaret Grace Rever 1934	Margaret	Grace	Rever	1934	Violet Sylvia Steward 1894	Charles Herbert Rever 1895
Mark Anthony Heath 1960	Mark	Anthony	Heath	1960	Eileen Mary Rever 1929	Dereck Heath
Mark Bright 1956	Mark	none	Bright	1956	Joyce Gosport	John Bright 1930
Nicholas Charles Heath 1964	Nicholas	Charles	Heath	1964	Eileen Mary Rever 1929	Dereck Heath
Nora Ada Bright 1899	Nora	Ada	Bright	1899	Charlotte Hewett 1863	Henry Edmund Bright 1862
Norman James Archer 1909	Norman	James	Archer	1909	Violet Heath 1887	James Alexander Archer 1882
Peter William Bright 1941	Peter	William	Bright	1941	Iris Ellen Archer 1906	William George Bright 1901
Richard John Bright 1962	Richard	John	Bright	1962	Margaret Grace Rever 1934	David Bright 1934
Robert David Bright 1965	Robert	David	Bright	1965	Margaret Grace Rever 1934	David Bright 1934
Violet Heath 1887	Violet	none	Heath	1887	not specified	not specified
Violet Sylvia Steward 1894	Violet	Sylvia	Steward	1894	Lois Green 1871	John Tacey Steward 1873
William Bright 1970	William	none	Bright	1970	Joyce Gosport	John Bright 1930
William George Bright 1901	William	George	Bright	1901	Charlotte Hewett 1863	Henry Edmund Bright 1862
William Rever 1870	William	none	Rever	1870	not specified	not specified

FHKB OWL Files for Download

Chapter	FHKB snapshot
2	download
3	download
4	download
5	download
6	download
7	download
8	download
9	download
10	download

Bibliography

[1] M. Horridge and S. Bechhofer. The owl api: a java api for working with owl 2 ontologies. Proc. of OWL Experiences and Directions , 2009, 2009.

[2] Luigi Iannone, Alan Rector, and Robert Stevens. Embedding knowledge patterns into owl. In European Semantic Web Conference (ESWC09) , pages 218–232, 2009.

[3] Dmitry Tsarkov, Uli Sattler, Margaret Stevens, and Robert Stevens. A Solution for the Man-Man Problem in the Family History Knowledge Base. In Sixth International Workshop on OWL: Experiences and Directions 2009 , 2009.