SubClassOf vs EquivalentTo¶
Prerequisites¶
This lesson assumes you have basic knowledge wrt ontologies and OWL as explained in:
SubClassOf¶
In this section we explain the semantics of SubClassOf, give an example of using SubClassOf and provide guidance for when not to use SubClassOf.
Semantics¶
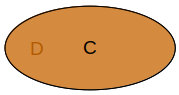
If we have
Class: C
SubClassOf: D
Class: D
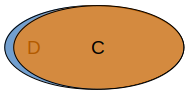
the semantics of it is given by the following Venn diagram:
Thus, the semantics is given by the subset relationship, stating the C is a subset of D. This means every individual
of C is necessarily an individual of D, but not every individual of D is necessarily an individual of C.
A concrete example¶
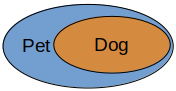
Class: Dog
SubClassOf: Pet
Class: Pet
which as a Venn diagram will look as follows:
Guidance¶
There are at least 2 scenarios which at first glance may seem like C SubClassOf D holds, but it does not hold, or
using C EquivalentTo D may be a better option.
- This is typically where
Chas many individuals that are inD, but there is at least 1 individual ofCthat is not inD. The following Venn diagram is an example. Thus, to check whether you may be dealing with this scenario, you can ask the following question: Is there any individual inCthat is not inD? If 'yes', you are dealing with this scanario and you should not be usingC SubClassOf D.
- When you have determined that (1) does not hold, you may deal with the scenario where not only is every individual of
CinD, but also every individual inDis inC. This meansCandDare equivalent. In the case you rather want to make use ofEquivalentTo.
EquivalentTo¶
Semantics¶
If we have
Class: C
EquivalentTo: D
Class: D
this means the sets C and D fit perfectly on each other, as shown in the next Venn diagram:

Note that C EquivalentTo D is shorthand for
Class: C
SubClassOf: D
Class: D
SubClassOf: C
though, in general it is better to use EquivalentTo rather than the 2 SubClassOf axioms when C and D are equivalent.
A concrete example¶
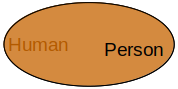
We all probably think of humans and persons as the exact same set of individuals.
Class: Person
EquivalentTo: Human
Class: Human
and as a Venn diagram:
Guidance¶
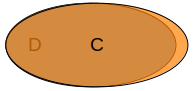
When do you not want to use EquivalentTo?
- When there is an individual of
Cthat is not inD.
- When there is an individual of
Dthat is not inC.